End of chapter exercises

Textbook Exercise 7.6

with centre $\left(0;5\right)$ and radius $\text{5}$

$\begin{align*} (x)^2 + (y-5)^2 &= 5^{2} \\ (x)^2 + (y-5)^2 &= 25 \\ & \\ \text{Expanded: } x^2 + y^2 -10y + 25 &= 25 \\ x^2 + y^2 - 10y &=0 \end{align*}$

with centre $\left(2;0\right)$ and radius $\text{4}$

$\begin{align*} (x-2)^2 + y^2 &= 16 \\ & \\ \text{Expanded: } x^2 -4x + 4 + y^2 &= 16 \\ x^2 - 4x + y^2 - 12 &= 0 \end{align*}$

with centre $\left(-5;7\right)$ and radius $\text{18}$

$\begin{align*} (x+5)^2 + (y-7)^2 &= 18^{2} \\ (x+5)^2 + (y-7)^2 &= 324\\ & \\ \text{Expanded: } x^2 + 10x + 25 + y^2 -14y + 49 &= 324 \\ x^2 + 10x + y^2 -14y - 250 &=0 \end{align*}$

with centre $\left(-2;0\right)$ and diameter $\text{6}$

$\begin{align*} (x+2)^2 + y^2 &= 9 \\ & \\ \text{Expanded: } x^2 + 4x + 4 + y^2 - 9 &= 0 \\ x^2 + 4x + y^2 - 5 &= 0 \end{align*}$

with centre $\left(-5;-3\right)$ and radius $\sqrt{3}$

$\begin{align*} (x+5)^2 + (y+3)^2 &= 3 \\ & \\ \text{Expanded: } x^2 + 10x + 25 + y^2 + 6y + 9 &= 3 \\ x^2 + 10x + y^2 + 6y + 31 &= 0 \end{align*}$

Find the equation of the circle with centre $\left(2;1\right)$ which passes through $\left(4;1\right)$ .

$\begin{align*} (x - 2)^2 + (y - 1)^2 &= r^{2} \\ (4 - 2)^2 + (1 - 1)^2 &= r^{2} \\ (2)^2 + (0)^2 &= r^{2} \\ 4 &= r^{2} \\ \therefore r &= 2 \\ (x - 2)^2 + (y - 1)^2 &= 4 \\ & \\ \text{Expanded: } x^2 - 4x + y^2 - 2y + 1 &= 0 \end{align*}$

Where does it cut the line $y=x+1$ ?

$\begin{align*} (x - 2)^2 + (y - 1)^2 &= 4 \\ (x - 2)^2 + (x + 1 - 1)^2 &= 4 \\ (x - 2)^2 + (x)^2 &= 4 \\ x^2 - 4x + 4 + x^2 &= 4 \\ 2x^2 - 4x &= 0 \\ x^2 - 2x &= 0 \\ x(x - 2) &= 0 \\ \therefore x = 0 &\text{ or } x = 2 \\ \text{If } x = 0, y &= 1 \quad (0;1) \\ \text{If } x = 2, y &= 3 \quad (2;3) \end{align*}$

Find the equation of the circle with centre $\left(-3;-2\right)$ which passes through $\left(1;-4\right)$ .

$\begin{align*} (x + 3)^2 + (y + 2)^2 &= r^{2} \\ (1 + 3)^2 + (-4 + 2)^2 &= r^{2} \\ (4)^2 + (-2)^2 &= r^{2} \\ 16 + 4 &= r^{2} \\ 20 &= r^{2} \\ (x + 3)^2 + (y + 2)^2 &= 20 \end{align*}$

Find the equation of the circle with centre $\left(3;1\right)$ which passes through $\left(2;5\right)$ .

$\begin{align*} (x - 3)^2 + (y - 1)^2 &= r^{2} \\ (2 - 3)^2 + (5 - 1)^2 &= r^{2} \\ (-1)^2 + (4)^2 &= r^{2} \\ 1 + 16 &= r^{2} \\ 17&= r^{2} \\ (x - 3)^2 + (y - 1)^2 &= 17 \end{align*}$

${\left(x+9\right)}^{2}+{\left(y-6\right)}^{2}=36$

$(-9;6)$ ,

$r = 6$ units

$\frac{1}{2}{\left(x-2\right)}^{2}+\frac{1}{2}{\left(y-9\right)}^{2}=1$

$(2;9)$ ,

$r = \sqrt{2}$ unit

${\left(x+5\right)}^{2}+{\left(y+7\right)}^{2}=12$

$(-5;-7)$ ,

$r = \sqrt{12}$ units

$x^{2}+{\left(y+4\right)}^{2}=23$

$(0;-4)$ ,

$r = \sqrt{23}$ units

$3{\left(x-2\right)}^{2}+3{\left(y+3\right)}^{2}=12$

$(2;-3)$ ,

$r = 2$ units

${x}^{2}+{\left(y-6\right)}^{2}=100$

$\begin{align*} {x}^{2}+{\left(y-6\right)}^{2}&=100 \\ \text{Let } x = 0: \quad {\left(y-6\right)}^{2}&=100 \\ y^{2} - 12y + 36 &= 100 \\ y^{2} - 12y - 64 &= 0 \\ (y - 16)(y + 4) &= 0 \\ \therefore y = 16 &\text{ or } y = -4 \\ (0;16) &\text{ and } (0;-4)\\ & \\ {x}^{2}+{\left(y-6\right)}^{2}&=100 \\ \text{Let } y = 0: \quad {x}^{2}+{\left(-6\right)}^{2}&=100 \\ {x}^{2}+ 36 &=100 \\ {x}^{2} &= 64 \\ \therefore x = -8 &\text{ or } x = 8 \\ (-8;0) &\text{ and } (8;0) \end{align*}$

${\left(x+4\right)}^{2}+{y}^{2}=16$

$\begin{align*} {\left(x+4\right)}^{2}+{y}^{2} &= 16 \\ \text{Let } x = 0: \quad {\left(x+4\right)}^{2}+{y}^{2} &= 16 \\ 4^{2} + y^{2} &= 16 \\ y^{2} &= 0 \\ \therefore & (0;0) \\ & \\ {\left(x+4\right)}^{2}+{y}^{2} &= 16 \\ \text{Let } y = 0: \quad ({x} + 4)^{2}&=16 \\ x^{2} + 8x + 16 &=16 \\ x^{2} + 8x &= 0 \\ x(x + 8) &= 0 \\ \therefore x = 0 &\text{ or } x = -8 \\ (0;0) &\text{ and } (-8;0) \end{align*}$

${x}^{2}+6x+{y}^{2}-12y=-20$

$\begin{align*} {x}^{2}+6x+{y}^{2}-12y &= -20 \\ ({x} + 3)^{2} - 9 + ({y} - 6)^{2} - 36 &= -20 \\ ({x} + 3)^{2} + ({y} - 6)^{2} &= 25 \end{align*}$

The centre of the circle is $(-3;6)$ and $r = 5$ units.

${x}^{2}+4x+{y}^{2}-8y=0$

$\begin{align*} {x}^{2}+4x+{y}^{2}-8y &= 0 \\ ({x} + 2)^{2} - 4 + ({y} - 4)^{2} - 16 &= 0 \\ ({x} + 2)^{2} + ({y} - 4)^{2} &= 20 \end{align*}$

The centre of the circle is $(-2;4)$ and $r = \sqrt{20}$ units.

${x}^{2}+{y}^{2}+8y=7$

$\begin{align*} {x}^{2}+{y}^{2}+8y &= 7 \\ {x}^{2} + ({y} + 4)^{2} - 16 &= 7 \\ {x}^{2} + ({y} + 4)^{2} &= 23 \end{align*}$

The centre of the circle is $(0;-4)$ and $r = \sqrt{23}$ units.

${x}^{2}-6x+{y}^{2}=16$

$\begin{align*} {x}^{2}-6x+{y}^{2} &= 16 \\ (x - 3)^{2} - 9 + y^{2} &= 16 \\ (x - 3)^{2} + y^{2} &= 25 \end{align*}$

The centre of the circle is $(3;0)$ and $r = 5$ units.

${x}^{2}-5x+{y}^{2}+3y=-\frac{3}{4}$

$\begin{align*} {x}^{2}-5x+{y}^{2}+3y &= -\frac{3}{4} \\ \left(x - \frac{5}{2}\right)^{2} - \frac{25}{4} + \left(y + \frac{3}{2}\right)^{2} - \frac{9}{4} &= -\frac{3}{4} \\ \left(x - \frac{5}{2}\right)^{2} + \left(y + \frac{3}{2}\right)^{2} &= \frac{31}{4} \end{align*}$

The centre of the circle is $(\frac{5}{2};-\frac{3}{2})$ and $r = \frac{\sqrt{31}}{2}$ units.

${x}^{2}-6nx+{y}^{2}+10ny=9{n}^{2}$

$\begin{align*} {x}^{2}-6nx+{y}^{2}+10ny &= 9{n}^{2} \\ (x - 3n)^{2} - 9n^{2} + (y + 5n)^{2} - 25n^{2} &= 9{n}^{2} \\ (x - 3n)^{2} + (y + 5n)^{2} &= 43{n}^{2} \end{align*}$

The centre of the circle is $(3n;-5n)$ and $r = \sqrt{43}n$ units.

Find the gradient of the radius between the point $(4;5)$ on the circle and its centre $(-8;4)$ .

Given:

the centre of the circle $(a;b) = (-8;4)$
a point on the circumference of the circle $(4;5)$

Required:

the gradient $m$ of the radius

$\begin{align*} m & = \frac{y_2 - y_1}{x_2 - x_1}\\ & = \frac{5-4}{4+8}\\ & = \frac{1}{12} \end{align*}$

The gradient for this radius is $m = \frac{1}{12}$ .

Find the gradient line tangent to the circle at the point $(4;5)$ .

The tangent to the circle at the point $(4;5)$ is perpendicular to the radius of the circle to that same point:

$\begin{align*} m_{\bot} & = - \frac{1}{m}\\ & = \frac{-1}{\frac{1}{12} }\\ & = -12 \end{align*}$

The gradient for the tangent is $m_{\bot} = -12$ .

Given $\left(x - 1\right)^{2} + \left(y - 7\right)^{2} = 10$ , determine the value(s) of $x$ if $(x;4)$ lies on the circle.

$\begin{align*} (x - 1)^{2} + (4 - 7)^{2} &= 10 \\ x^{2} - 2x + 1 + 9 &= 10 \\ x(x - 2) &= 0 \\ \therefore x = 0 &\text{ or } x = 2 \end{align*}$

The points $(0;4)$ and $(2;4)$ lie on the circle.

$(0;4),(2;4)$

Find the gradient of the tangent to the circle at the point $(2;4)$ .

$\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{4 - 7}{2 - 1} \\ & = -3 \end{align*}$

$\begin{align*} m_{\text{tangent}} & = - \frac{1}{m}\\ & = - \dfrac{1}{-3}\\ \\ & = \frac{1}{3} \end{align*}$

The gradient of the tangent is $m_{\text{tangent}} = \frac{1}{3}$ .

$m = \frac{1}{3}$

Given a circle with the central coordinates $(a;b) = (-2;-2)$ . Determine the equation of the tangent line of the circle at the point $(-1;3)$ .

$\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{3 - (-2)}{-1 -(-2)} \\ & = 5 \end{align*}$

The radius is perpendicular to the tangent, therefore $m_{r} \times m_{\bot} = -1$ :

$m_{\bot} = - \frac{1}{5}$

Substitute $m = - \frac{1}{5}$ and $(-1;3)$ to determine $c$ :

$\begin{align*} y & =m_{\bot} x + c\\ 3 & = - \frac{1}{5} (-1) + c \\ c & = \frac{14}{5} \end{align*}$

The equation of the tangent to the circle at the point $(-1;3)$ is $y = - \frac{1}{5} x + \frac{14}{5}$ .

$y = - \frac{1}{5} x + \frac{14}{5}$

Consider the diagram below:

Find the equation of the tangent to the circle at point $T$ .

$\begin{align*} m_r & = \frac{y_{1} - y_0}{x_{1} - x_0} \\ & = \frac{4+5}{4+3 } \\ & = \frac{9}{7} \end{align*}$

$\begin{align*} m_r \times m & = -1 \\ \therefore m & = - \frac{1}{m_r} \\ & = - \dfrac{1}{\frac{9}{7} } \\ & = - \frac{7}{9} \end{align*}$

Determine the $y$ -intercept ( $c$ ) of the line by substituting the point $T(-3;-5)$ .

$\begin{align*} y & = m x + c\\ -5 & = - \frac{7}{9} (-3) + c \\ c & = - \frac{22}{3} \end{align*}$

The equation of the tangent to the circle at $T$ is

$\begin{align*} y & = - \frac{7}{9} x - \frac{22}{3} \end{align*}$

$y = - \frac{7}{9} x - \frac{22}{3}$

$M(-2;-5)$ is a point on the circle $x^{2} + y^{2} + 18y + 61 = 0$ . Determine the equation of the tangent at $M$ .

Complete the square:

$\begin{align*} x^{2} + y^{2} + 18y + 61 &= 0 \\ x^{2} + (y^{2} + 18y) &= -61 \\ x^{2} + (y + 9)^{2} - 81 &= -61 \\ x^{2} + (y + 9)^{2} &= 20 \end{align*}$

Therefore the centre of the circle is $(0;-9)$ and $r = \sqrt{20}$ units.

Calculate the gradient of the radius:

$\begin{align*} m_r & = \frac{y_1 - y_0}{x_1 - x_0} \\ & = \frac{-5 - (-9)}{-2 - 0} \\ & = \frac{4}{-2} \\ & = -2 \end{align*}$

$\begin{align*} m_{\bot} & = - \frac{1}{m_r} \\ & = - \frac{1}{-2} \\ & = \frac{1}{2} \end{align*}$

Determine the $y$ -intercept $c$ of the line by substituting the point $M(-2;-5)$ .

$\begin{align*} y & = m_{\bot} x + c\\ -5 & = \frac{1}{2} (-2) + c \\ c & = -4 \end{align*}$

The equation for the tangent to the circle at the point $M(-2;-5)$ is

$\begin{align*} y & = \frac{1}{2} x - 4 \end{align*}$

$y = \frac{1}{2} x - 4$

Find the equation of the circle given.

$\begin{align*} r & = \sqrt{(x_1 - x_0)^2 + (y_1 - y_0)^2} \\ & = \sqrt{(2+4)^2 + (-3-2)^2} \\ & = \sqrt{(6)^2 + (-5)^2} \\ & = \sqrt{61} \end{align*}$

$\begin{align*} (x-a)^2+ (y-b)^2 & = r^2 \\ (x - (-4))^2 + (y-(2))^2 & = (\sqrt{61})^2 \\ \left(x + 4\right)^{2} + \left(y - 2\right)^{2} & = 61 \end{align*}$

The equation of the circle is $\left(x + 4\right)^{2} + \left(y - 2\right)^{2} = 61$ .

$\left(x + 4\right)^{2} + \left(y - 2\right)^{2} = 61$

Determine the value of $p$ .

$\begin{align*} \left(x + 4\right)^{2} + \left(y - 2\right)^{2} & = 61 \\ \left(-10 + 4\right)^{2} + \left(p - 2\right)^{2} & = 61 \\ \left(-10 + 4\right)^{2} + p^{2} - 4p + 4 & = 61 \\ 36 + p^{2} - 4p + 4 & = 61 \\ p^{2} - 4p - 21 & = 0 \\ (p+3)(p-7) & = 0 \\ \therefore p = -3 & \text{ or } p = 7 \end{align*}$

From the graph we see that the correct $y$ -value is $-\text{3}$ .

The coordinates for point $Q$ is $Q(-10;-3)$

$p = -3$

Determine the equation of the tangent to the circle at point $Q$ .

$\begin{align*} m_r & = \frac{y_2 - y_0}{x_2 - x_0} \\ & = \frac{-3 -2}{-10 -(-4) } \\ & = \frac{5}{6} \end{align*}$

$m_{r} \times m_{\bot} = -1$ .

$\begin{align*} m_{\bot} & = - \frac{1}{m_r} \\ & = - \dfrac{1}{\frac{5}{6}} \\ & = - \frac{6}{5} \end{align*}$

Determine the $y$ -intercept $c$ of the line by substituting the point $Q(x_2;y_2) = (-10;-3)$ .

$\begin{align*} y_2 & = m_{\bot} x_2 + c\\ -3 & = - \frac{6}{5} (-10) + c \\ c & = -15 \end{align*}$

The equation of the tangent to the circle at $Q$ is $y = - \frac{6}{5} x - 15$ .

${x}^{2}+{y}^{2}=17$ at the point $\left(1;4\right)$

The centre of the circle is $(0;0)$ and $r = \sqrt{17}$ units.

$\begin{align*} m_{r} & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \frac{4 - 0}{1 - 0} \\ & = 4 \end{align*}$

$\begin{align*} m_{r} & \times m_{\bot} = -1 \\ m_{\bot} & = - \frac{1}{m_{r}} \\ & = - \dfrac{1}{4} \\ & = - \frac{1}{4} \end{align*}$

$\begin{align*} y_2 & = m_{\bot} x_2 + c\\ 4 & = - \frac{1}{4}(1) + c \\ c & = \frac{17}{4} \end{align*}$

The equation of the tangent to the circle is $y = - \frac{1}{4} x + \frac{17}{4}$ .

${x}^{2}+{y}^{2}=25$ at the point $\left(3;4\right)$

The centre of the circle is $(0;0)$ and $r = 5$ units.

$\begin{align*} m_{r} & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \frac{4 - 0}{3 - 0} \\ & = \frac{4}{3} \end{align*}$

$\begin{align*} m_{r} & \times m_{\bot} = -1 \\ m_{\bot} & = - \frac{1}{m_{r}} \\ & = - \dfrac{1}{\frac{4}{3} } \\ & = - \frac{3}{4} \end{align*}$

$\begin{align*} y_2 & = m_{\bot} x_2 + c\\ 4 & = - \frac{3}{4}(3) + c \\ c & = \frac{25}{4} \end{align*}$

The equation of the tangent to the circle is $y = - \frac{3}{4} x + \frac{25}{4}$ .

${\left(x+1\right)}^{2}+{\left(y-2\right)}^{2}=25$ at the point $\left(3;5\right)$

The centre of the circle is $(-1;2)$ and $r = 5$ units.

$\begin{align*} m_{r} & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \frac{5-2}{3 - (-1)} \\ & = \frac{3}{4} \end{align*}$

$\begin{align*} m_{r} & \times m_{\bot} = -1 \\ m_{\bot} & = - \frac{1}{m_{r}} \\ & = - \dfrac{1}{\frac{3}{4} } \\ & = - \frac{4}{3} \end{align*}$

$\begin{align*} y_2 & = m_{\bot} x_2 + c\\ 5 & = - \frac{4}{3}(3) + c \\ c & = 9 \end{align*}$

The equation of the tangent to the circle is $y = - \frac{4}{3} x + 9$ .

${\left(x-2\right)}^{2}+{\left(y-1\right)}^{2}=13$ at the point $\left(5;3\right)$

The centre of the circle is $(2;1)$ and $r = \sqrt{13}$ units.

$\begin{align*} m_{r} & = \frac{y_2 - y_1}{x_2 - x_1} \\ & = \frac{3-1}{5-2} \\ & = \frac{2}{3} \end{align*}$

$\begin{align*} m_{r} & \times m_{\bot} = -1 \\ m_{\bot} & = - \frac{1}{m_{r}} \\ & = - \dfrac{1}{\frac{2}{3} } \\ & = - \frac{3}{2} \end{align*}$

$\begin{align*} y_2 & = m_{\bot} x_2 + c\\ 3 & = - \frac{3}{2}(5) + c \\ c & = \frac{21}{2} \end{align*}$

The equation of the tangent to the circle is $y = - \frac{3}{2} x + \frac{21}{2}$ .

Determine the equations of the tangents to the circle $x^{2} + y^{2} = 50$ , given that both lines have an angle of inclination of $\text{45} °$ .

The centre of the circle is $(0;0)$ and $r = \sqrt{50}$ units.

Gradient of the tangents:

$\begin{align*} m & = \tan \theta \\ & = \tan{ \text{45} °} \\ & = 1 \end{align*}$

$\begin{align*} m & \times m_{\bot} = -1 \\ m & = - 1 \end{align*}$

The line perpendicular to the tangents and passing through the centre of the circle is $y = -x$ . Substitute $y = -x$ into the equation of the circle and solve for $x$ :

$\begin{align*} x^{2} + (-x)^{2} &= 50 \\ 2x^{2} &= 50 \\ x^{2} &= 25 \\ x &= \pm 5 \end{align*}$

This gives the points $P(-5;5)$ and $Q(5;-5)$ .

Tangent at $P(-5;5)$ :

$\begin{align*} y - 5 & = (1)(x - (-5)) \\ y & = x + 10 \end{align*}$

Tangent at $Q(5;-5)$ :

$\begin{align*} y - (-5) & = (1)(x - 5) \\ y & = x - 10 \end{align*}$

The equations of the tangents to the circle are $y = x - 10$ and $y = x + 10$ .

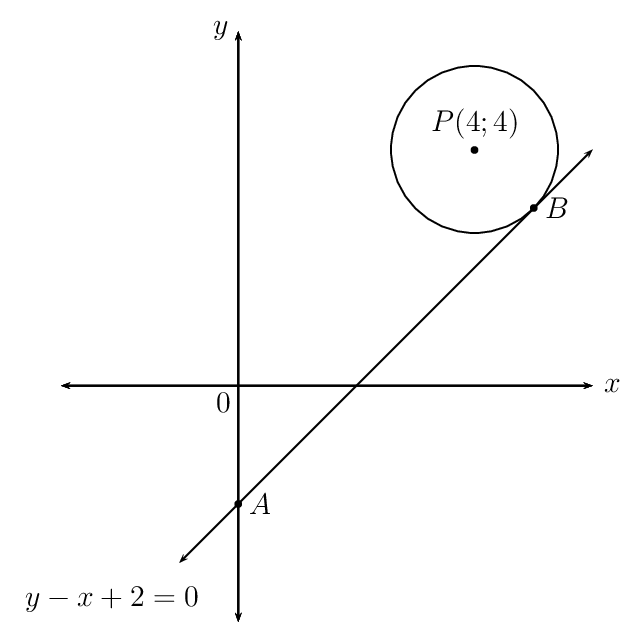
Determine the equation of $PB$ .

$\begin{align*} m_{AB} & = 1 \\ \therefore m_{PB} & = - 1 \\ y & = mx + c \\ \text{Substitute } P(4;4): \quad 4 & = -(4) + c \\ \therefore c &= 8 \\ y &= -x + 8 \end{align*}$

$y = -x + 8$

Determine the coordinates of $B$ .

Equate the two equations and solve for $x$ :

$\begin{align*} x -2 & = -x + 8 \\ 2x & = 10 \\ x & = 5 \\ y &= -5 + 8 \\ \therefore y &= 3 \end{align*}$

$B(5;3)$

Determine the equation of the circle.

$\begin{align*} PB^{2} & = (5 -4)^{2} + (3 - 4)^{2} \\ & = 1 + 1 \\ & = 2 \\ (x -4)^{2} + (y - 4)^{2} & = 2 \end{align*}$

$(x -4)^{2} + (y - 4)^{2} = 2$

Describe in words how the circle must be shifted so that $P$ is at the origin.

The circle must be shifted

$\text{4}$ units down and

$\text{4}$ units to the left.

If the length of $PB$ is tripled and the circle is shifted $\text{2}$ units to the right and $\text{1}$ unit up, determine the equation of the new circle.

$\begin{align*} PB & = \sqrt{2} \\ 3 \times PB & = 3\sqrt{2} \\ \text{Horizontal shift: } (x -4 - 2)^{2} + (y - 4)^{2} & = \left( 3\sqrt{2} \right)^2 \\ (x -6)^{2} + (y - 4)^{2} & = 9(2) \\ \text{Vertical shift: } (x -6)^{2} + (y - 4 -1)^{2} & = 18 \\ (x -6)^{2} + (y - 5)^{2} & = 18 \end{align*}$

The equation of a circle with centre $A$ is $x^{2} + y^{2} + 5 = 16x + 8y - 30$ and the equation of a circle with centre $B$ is $5x^{2} + 5y^{2} = 25$ . Prove that the two circles touch each other.

$\begin{align*} x^{2} + y^{2} + 5 & = 16x + 8y - 30 \\ x^{2} -16x + y^{2} - 8y & = - 35 \\ (x - 8)^{2} -64 + (y - 4)^{2} -16 & = - 35 \\ (x - 8)^{2} + (y - 4)^{2} & = 45 \\ & \\ 5x^{2} + 5y^{2} &= 25 \\ x^{2} + y^{2} &= 5 \\ & \\ AB^{2} &= (8 - 0)^{2} + (4 - 0)^{2} \\ &= 64 + 16 \\ &= 80\\ \therefore AB &= \sqrt{80} \\ AB &= 4\sqrt{5} \\ & \\ \text{And } \text{radius}_{A} + \text{radius}_{B} &= \sqrt{45} + \sqrt{5} \\ &= 3\sqrt{5} + \sqrt{5} \\ &= 4\sqrt{5} \\ &=AB \end{align*}$

Therefore the two circles touch each other.

7.4 Summary

Table of Contents

8.1 Revision