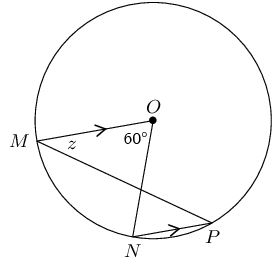
\(MO \parallel NP\) in a circle with centre \(O\). \(M\hat{O}N = \text{60}°\) and \(O\hat{M}P = z\). Calculate the value of \(z\), giving reasons.

We think you are located in United States. Is this correct?
We use this information to present the correct curriculum and to personalise content to better meet the needs of our users.
|
Previous
End of chapter exercises
|
Next
8.2 Ratio and proportion
|
|
Name |
Diagram |
Properties |
|
Scalene |
 |
All sides and angles are different. |
|
Isosceles |
 |
Two sides are equal in length. The angles opposite the equal sides are also equal. |
|
Equilateral |
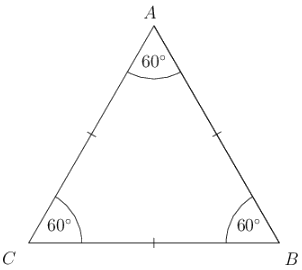 |
All three sides are equal in length and all three angles are equal. |
|
Acute-angled |
 |
Each of the three interior angles is less than \(\text{90}\)°. |
|
Obtuse-angled |
 |
One interior angle is greater than \(\text{90}\)°. |
|
Right-angled |
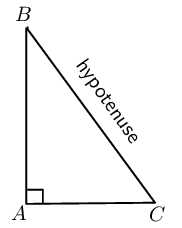 |
One interior angle is \(\text{90}\)°. |
|
Condition |
Diagram |
|
SSS (side, side, side) |
\(\triangle ABC \equiv \triangle EDF\) |
|
SAS (side, incl. angle, side) |
\(\triangle GHI \equiv \triangle JKL\) |
|
AAS (angle, angle, side) |
\(\triangle MNO \equiv \triangle PQR\) |
|
RHS (\(\text{90}\)°, hypotenuse, side) |
\(\triangle STU \equiv \triangle VWX\) |
|
Condition |
Diagram |
|
AAA (angle, angle, angle) |
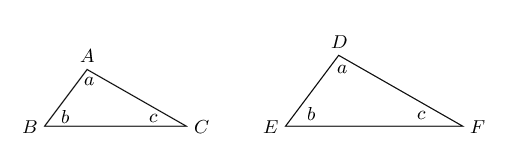
\(\hat{A} = \hat{D}, \enspace \hat{B} = \hat{E}, \enspace \hat{C} = \hat{F}\) \(\therefore \triangle ABC \enspace ||| \enspace \triangle DEF\) |
|
SSS (sides in prop.) |
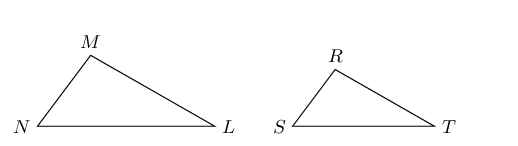
\(\frac{MN}{RS} = \frac{ML}{RT} = \frac{NL}{ST}\) \(\therefore \triangle MNL \enspace ||| \enspace \triangle RST\) |
 |
|
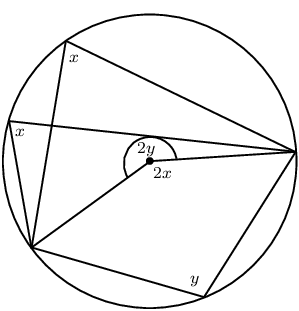 |
If an arc subtends an angle at the centre of a circle and at the circumference, then the angle at the centre is twice the size of the angle at the circumference. |
 |
Angles at the circumference subtended by arcs of equal length (or by the same arc) are equal. |
 |
If the four sides of a quadrilateral \(ABCD\) are the chords of a circle with centre \(O\), then:
|
Proving a quadrilateral is cyclic:
 |
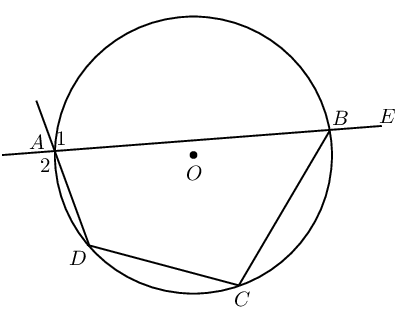
If \(\hat{A} + \hat{C} = \text{180}°\) or \(\hat{B} + \hat{D} = \text{180}°\), then \(ABCD\) is a cyclic quadrilateral. |
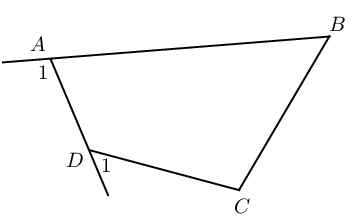 |
If \(\hat{A}_1 = \hat{C}\) or \(\hat{D}_1 = \hat{B}\), then \(ABCD\) is a cyclic quadrilateral. |
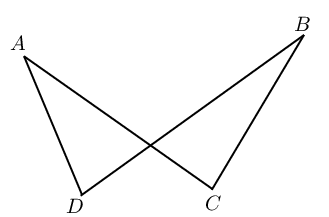 |
If \(\hat{A} = \hat{B}\) or \(\hat{C} = \hat{D}\), then \(ABCD\) is a cyclic quadrilateral. |
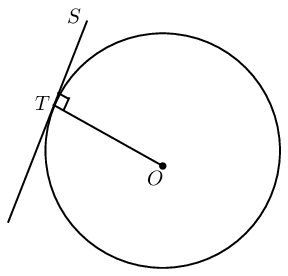 |
A tangent is perpendicular to the radius (\(OT \perp ST\)), drawn to the point of contact with the circle. |
 |
If \(AT\) and \(BT\) are tangents to a circle with centre \(O\), then:
|
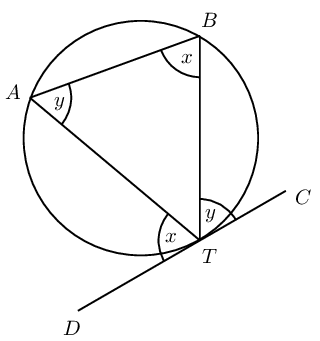 |
|
The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.
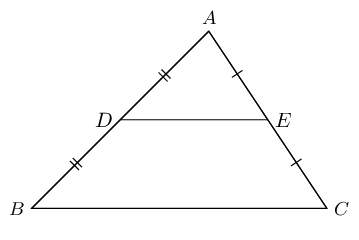
Given: \(AD = DB\) and \(AE = EC\), we can conclude that \(DE \parallel BC\) and \(DE = \frac{1}{2}BC\).
\(MO \parallel NP\) in a circle with centre \(O\). \(M\hat{O}N = \text{60}°\) and \(O\hat{M}P = z\). Calculate the value of \(z\), giving reasons.

\(O\) is the centre of the circle with \(OC = \text{5}\text{ cm}\) and chord \(BC = \text{8}\text{ cm}\).
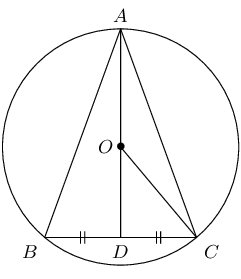
Determine the lengths of:
\(PQ\) is a diameter of the circle with centre \(O\). \(SQ\) bisects \(P\hat{Q}R\) and \(P\hat{Q}S = a\).
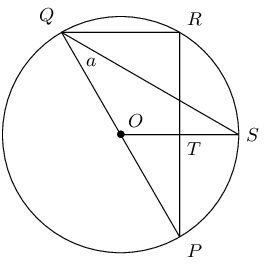
Write down two other angles that are also equal to \(a\).
Calculate \(P\hat{O}S\) in terms of \(a\), giving reasons.
Prove that \(OS\) is a perpendicular bisector of \(PR\).
\(BD\) is a diameter of the circle with centre \(O\). \(AB = AD\) and \(O\hat{C}D = \text{35}°\).
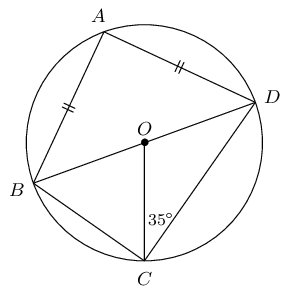
Calculate the value of the following angles, giving reasons:
\(O\) is the centre of the circle with diameter \(AB\). \(CD \perp AB\) at \(P\) and chord \(DE\) intersects \(AB\) at \(F\).
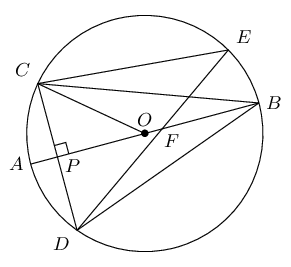
Prove the following:
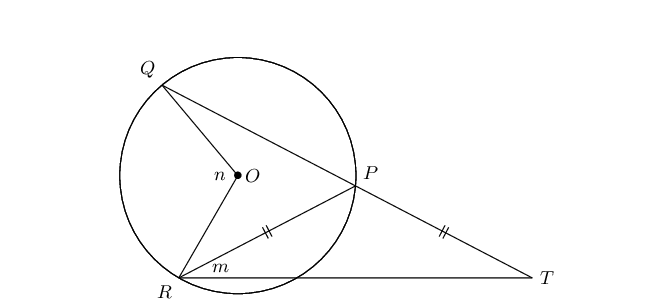
\(QP\) in the circle with centre \(O\) is extended to \(T\) so that \(PR = PT\). Express \(m\) in terms of \(n\).
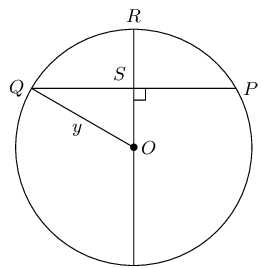
In the circle with centre \(O\), \(OR \perp QP\), \(QP = \text{30}\text{ mm}\) and \(RS = \text{9}\text{ mm}\). Determine the length of \(y\).
\(PQ\) is a diameter of the circle with centre \(O\). \(QP\) is extended to \(A\) and \(AC\) is a tangent to the circle. \(BA \perp AQ\) and \(BCQ\) is a straight line.

Prove the following:
\(BAPC\) is a cyclic quadrilateral
\(TA\) and \(TB\) are tangents to the circle with centre \(O\). \(C\) is a point on the circumference and \(A\hat{T}B = x\).
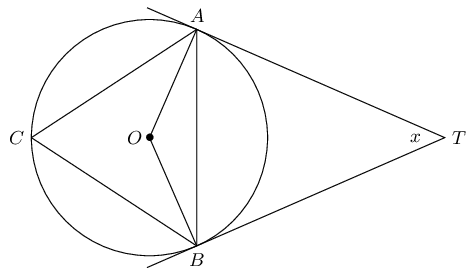
Express the following in terms of \(x\), giving reasons:
|
Previous
End of chapter exercises
|
Table of Contents |
Next
8.2 Ratio and proportion
|