7.4 Summary
|
Previous
7.3 Equation of a tangent to a circle
|
Next
End of chapter exercises
|
7.4 Summary (EMCHX)

| Theorem of Pythagoras: | AB2=AC2+BC2 |
| Distance formula: | AB=√(x2−x1)2+(y2−y1)2 |
| Gradient: | mAB=y2−y1x2−x1 or mAB=y1−y2x1−x2 |
| Mid-point of a line segment: | M(x;y)=(x1+x22;y1+y22) |
| Points on a straight line: | mAB=mAM=mMB |
| Straight line equations | Formulae |
| Two-point form: | y−y1x−x1=y2−y1x2−x1 |
| Gradient-point form: | y−y1=m(x−x1) |
| Gradient-intercept form: | y=mx+c |
| Horizontal lines: | y=k |
| Vertical lines | x=k |
| Parallel lines | 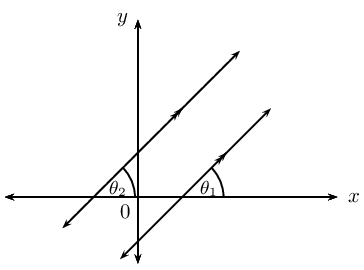 |
m1=m2 | θ1=θ2 |
| Perpendicular lines | 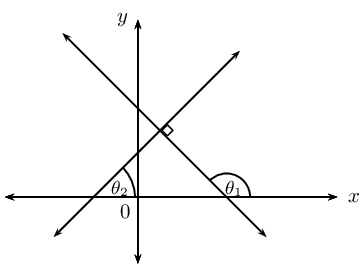 |
m1×m2=−1 | θ1=90°+θ2 |
-
Inclination of a straight line: the gradient of a straight line is equal to the tangent of the angle formed between the line and the positive direction of the x-axis.
m=tanθ for 0°≤θ<180°
-
Equation of a circle with centre at the origin:
If P(x;y) is a point on a circle with centre O(0;0) and radius r, then the equation of the circle is:
x2+y2=r2 -
General equation of a circle with centre at (a;b):
If P(x;y) is a point on a circle with centre C(a;b) and radius r, then the equation of the circle is:
(x−a)2+(y−b)2=r2 -
A tangent is a straight line that touches the circumference of a circle at only one point.
-
The radius of a circle is perpendicular to the tangent at the point of contact.
|
Previous
7.3 Equation of a tangent to a circle
|
Table of Contents |
Next
End of chapter exercises
|
