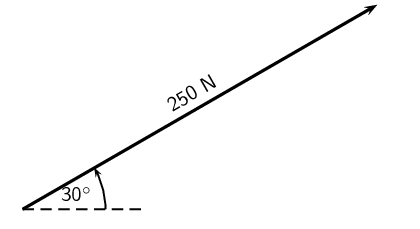
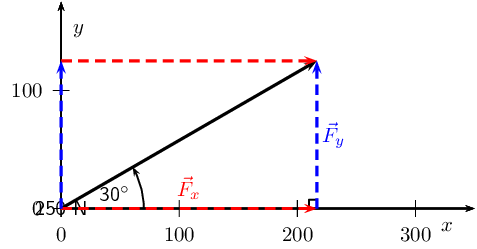
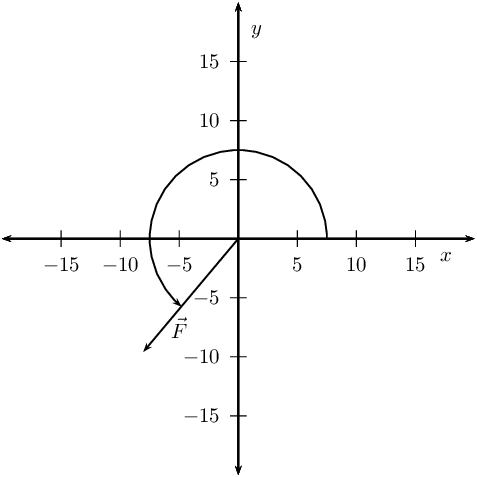
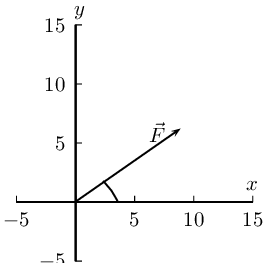
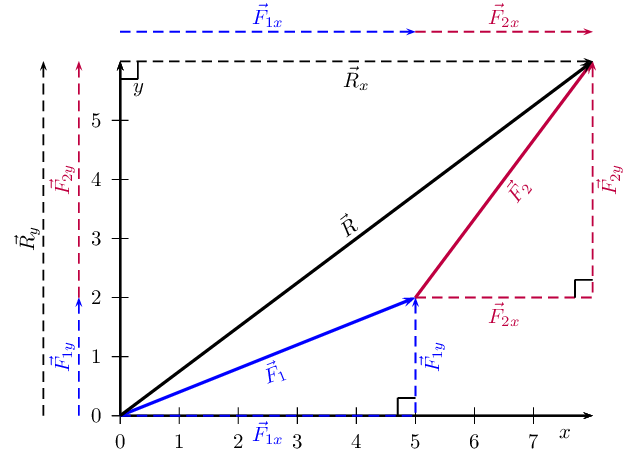
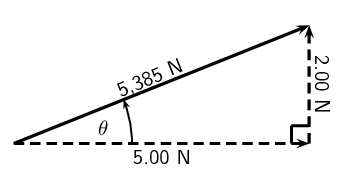
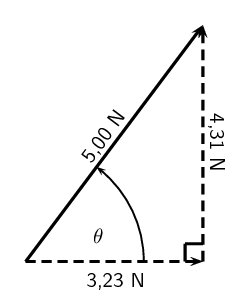
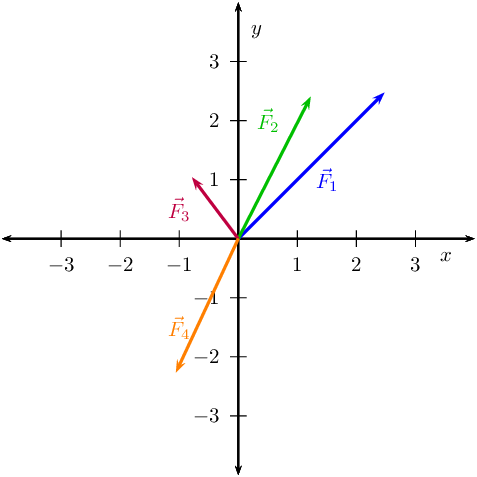
Resolve each of the following vectors into components:
- \(\vec{F}_1\)=\(\text{5}\) \(\text{N}\) at \(\text{45}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_2\)=\(\text{15}\) \(\text{N}\) at \(\text{63}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_3\)=\(\text{11,3}\) \(\text{N}\) at \(\text{127}\)\(\text{°}\) to the positive \(x\)-axis.
- \(\vec{F}_4\)=\(\text{125}\) \(\text{N}\) at \(\text{245}\)\(\text{°}\) to the positive \(x\)-axis.
-
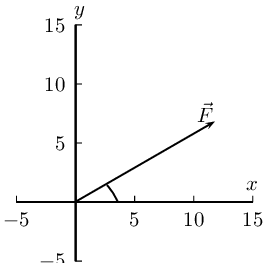
Draw a rough sketch of the original vector (we use a scale of \(\text{1}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\))
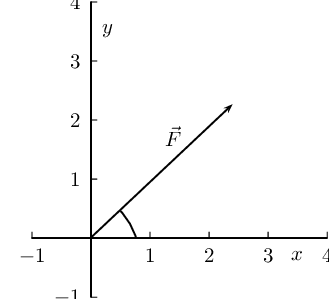
Next we resolve the force into components parallel to the axes. Since these directions are perpendicular to one another, the components form a right-angled triangle with the original force as its hypotenuse.
Now we can use trigonometry to calculate the magnitudes of the components of the original force:
\begin{align*} F_y &= 5 \sin(\text{45}\text{°})\\ &=\text{3,54}\text{ N} \end{align*}
and
\begin{align*} F_x &= 5 \cos(\text{45}\text{°})\\ &=\text{3,54}\text{ N} \end{align*}
-
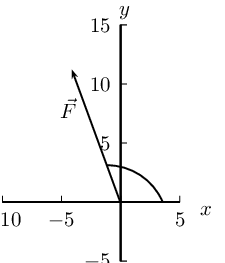
Draw a rough sketch of the original vector (we use a scale of \(\text{5}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\))
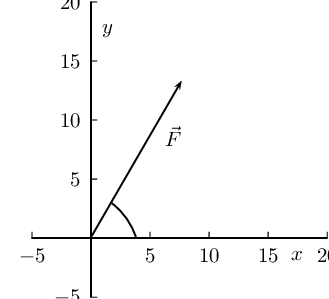
Next we resolve the force into components parallel to the axes. Since these directions are perpendicular to one another, the components form a right-angled triangle with the original force as its hypotenuse.
Now we can use trigonometry to calculate the magnitudes of the components of the original force:
\begin{align*} F_y &= 15 \sin(\text{63}\text{°})\\ &=\text{13,37}\text{ N} \end{align*}
and
\begin{align*} F_x &= 15 \cos(\text{63}\text{°})\\ &=\text{6,81}\text{ N} \end{align*}
-
Draw a rough sketch of the original vector (we use a scale of \(\text{4}\) \(\text{N}\) : \(\text{1}\) \(\text{cm}\))
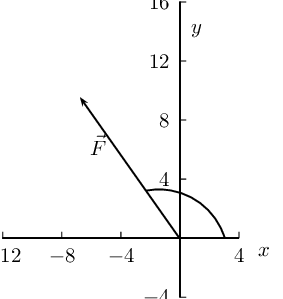
Next we resolve the force into components parallel to the axes. Since these directions are perpendicular to one another, the components form a right-angled triangle with the original force as its hypotenuse.
Now we can use trigonometry to calculate the magnitudes of the components of the original force:
\begin{align*} F_y &= \text{11,3} \sin(\text{127}\text{°})\\ &=\text{9,02}\text{ N} \end{align*}
and
\begin{align*} F_x &= \text{11,3} \cos(\text{127}\text{°})\\ &=-\text{6,80}\text{ N} \end{align*}
-
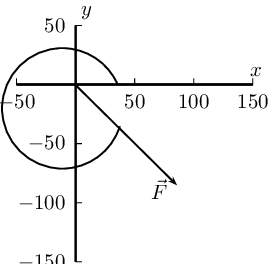
Draw a rough sketch of the original vector (we use a scale of \(\text{1}\) \(\text{cm}\) = \(\text{50}\) \(\text{N}\))

Next we resolve the force into components parallel to the axes. Since these directions are perpendicular to one another, the components form a right-angled triangle with the original force as its hypotenuse.
Now we can use trigonometry to calculate the magnitudes of the components of the original force:
\begin{align*} F_y &= \text{125} \sin(\text{245}\text{°})\\ &=-\text{113,29}\text{ N} \end{align*}
and
\begin{align*} F_x &= \text{125} \cos(\text{245}\text{°})\\ &=-\text{52,83}\text{ N} \end{align*}