2.4 Linear functions | Functions

2.4 Linear functions (EMCF9)

Inverse of the function $y=ax+q$ (EMCFB)

Worked example 4: Inverse of the function $y=ax+q$

Determine the inverse function of $p(x) = -3x + 1$ and sketch the graphs of $p(x)$ and $p^{-1}(x)$ on the same system of axes.

Determine the inverse of the given function

Interchange $x$ and $y$ in the equation.
Make $y$ the subject of the new equation.
Express the new equation in function notation.

$\begin{align*} \text{Let } y & = -3x + 1 \\ \text{Interchange } x \text{ and } y: \quad x & = -3y + 1 \\ x - 1 & = -3y \\ -\frac{1}{3}(x - 1) & = y \\ \therefore y &= -\frac{x}{3} + \frac{1}{3} \end{align*}$

Therefore, $p^{-1}(x) = -\frac{x}{3} + \frac{1}{3}$ .

Sketch the graphs of the same system of axes

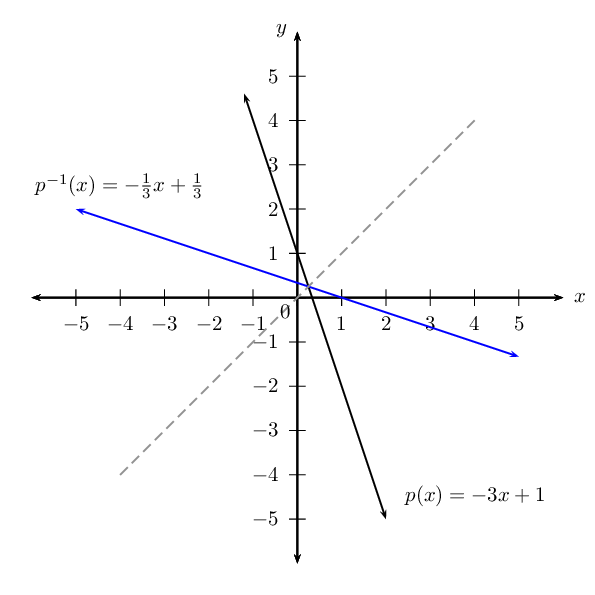
The graph of $p^{-1}(x)$ is the reflection of $p(x)$ about the line $y = x$ . This means that every point on the graph of $p(x)$ has a mirror image on the graph of $p^{-1}(x)$ .

To determine the inverse function of $y=ax+q$ :

$\begin{array}{rll} &(1) \quad \text{Interchange } x \text{ and } y: & x = ay+q \\ &(2) \quad \text{Make } y \text{ the subject of the equation}: & x - q = ay \\ && \frac{x}{a} - \frac{q}{a} = \frac{ay}{a} \\ &&\therefore y = \frac{1}{a}x-\frac{q}{a} \end{array}$

Therefore the inverse of $y=ax+q$ is $y=\frac{1}{a}x-\frac{q}{a}$ . If a linear function is invertible, then its inverse will also be linear.

Worked example 5: Inverses - domain, range and intercepts

Determine and sketch the inverse of the function $f(x) = 2x - 3$ . State the domain, range and intercepts.

Determine the inverse of the given function

Interchange $x$ and $y$ in the equation.
Make $y$ the subject of the new equation.
Express the new equation in function notation.

$\begin{align*} \text{Let } y & = 2x - 3 \\ \text{Interchange } x \text{ and } y: \quad x & = 2y - 3 \\ x + 3 & = 2y \\ \frac{1}{2}(x + 3) & = y \\ \therefore y &= \frac{x}{2} + \frac{3}{2} \end{align*}$

Therefore, $f^{-1}(x) = \frac{x}{2} + \frac{3}{2}$ .

Sketch the graphs on the same system of axes

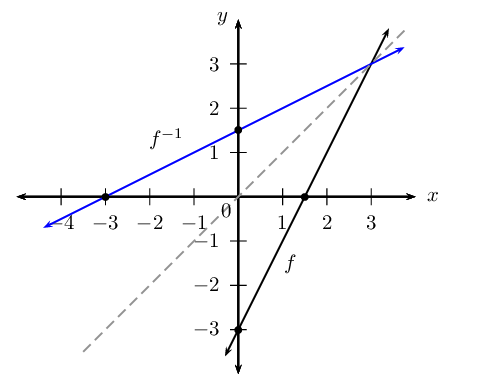
The graph of $f^{-1}(x)$ is the reflection of $f(x)$ about the line $y = x$ .

Determine domain, range and intercepts

$\begin{align*} \text{Domain of } f &: \{ x: x \in \mathbb{R} \} \\ \text{Range of } f &: \{ y: y \in \mathbb{R} \} \\ \text{Intercepts of } f &: (0;-3) \text{ and } \left(\frac{3}{2}; 0 \right) \\ & \\ \text{Domain of } f^{-1} &: \{ x: x \in \mathbb{R} \} \\ \text{Range of } f^{-1} &: \{ y: y \in \mathbb{R} \} \\ \text{Intercepts of } f^{-1} &: \left(0;\frac{3}{2}\right) \text{ and } (-3;0) \end{align*}$

Notice that the intercepts of $f$ and $f^{-1}$ are mirror images of each other. In other words, the $x$ - and $y$ -values have “swapped” positions. This is true of every point on the two graphs.

Domain and range

For a function of the form $y=ax+q$ , the domain is $\left\{x:x\in ℝ\right\}$ and the range is $\left\{y:y\in ℝ\right\}$ . When a function is inverted the domain and range are interchanged. Therefore, the domain and range of the inverse of an invertible, linear function will be $\left\{x:x\in ℝ\right\}$ and $\left\{y:y\in ℝ\right\}$ respectively.

Intercepts

The general form of an invertible, linear function is $y=ax+q \enspace (a \ne 0)$ and its inverse is $y=\frac{1}{a}x-\frac{q}{a}$ .

The $y$ -intercept is obtained by letting $x=0$ :

$\begin{align*} y &= \frac{1}{a}(0)-\frac{q}{a} \\ y &= -\frac{q}{a} \end{align*}$

This gives the point $\left(0; -\frac{q}{a}\right)$ .

The $x$ -intercept is obtained by letting $y=0$ :

$\begin{align*} 0 &= \frac{1}{a}x -\frac{q}{a} \\ \frac{q}{a} &= \frac{1}{a}x \\ q &= x \end{align*}$

This gives the point $(q; 0)$ .

It is interesting to note that if $f\left(x\right)=ax+q \enspace (a \ne 0)$ , then ${f}^{-1}\left(x\right)=\frac{1}{a}x-\frac{q}{a}$ and the $y$ -intercept of $f\left(x\right)$ is the $x$ -intercept of ${f}^{-1}\left(x\right)$ and the $x$ -intercept of $f\left(x\right)$ is the $y$ -intercept of ${f}^{-1}\left(x\right)$ .

Video: 28B3

Inverse of the function $y = ax + q$

Textbook Exercise 2.3

Given $f\left(x\right)=5x + 4$, find ${f}^{-1}\left(x\right)$.

\begin{align*} f(x): y & = 5x + 4 \\ f^{-1}(x): x & = 5y + 4 \\ \therefore x - 4 & = 5y \\ y & = \frac{1}{5}x - \frac{4}{5}\\ \therefore f^{-1}(x) & = \frac{1}{5}x - \frac{4}{5} \end{align*}

Is the relation a function? Explain your answer.

It is a function. Every $x$-value relates to only one $y$-value, it is a one-to-one relation.

Identify the domain and range.

\begin{align*} \text{Domain } & \{ x: x \in \mathbb{R} \} \\ \text{Range } & \{ y: y \in \mathbb{R} \} \end{align*}

Determine $f^{-1}(x)$.

\begin{align*} f(x): y & = -3x-7 \\ f^{-1}(x): x & = -3y-7 \\ \therefore x + 7 & = -3y \\ y & = - \frac{1}{3}x - \frac{7}{3} \\ \therefore f^{-1}(x) & = - \frac{1}{3}x - \frac{7}{3} \end{align*}

Sketch the graph of the function $f\left(x\right)=3x-1$ and its inverse on the same system of axes. Indicate the intercepts and the axis of symmetry of the two graphs.

\begin{align*} y & = 3x - 1 \\ x & = 3y - 1\\ \therefore 3y & = x + 1 \\ y & = \frac{1}{3}x + \frac{1}{3} \end{align*}

The intercepts are:

\begin{align*} f(x): x = 0, y = -\text{1}\\ y=0, x = \frac{1}{3}\\ f^{-1}(x): x = 0, y = \frac{1}{3}\\ y = 0, x = -\text{1} \end{align*}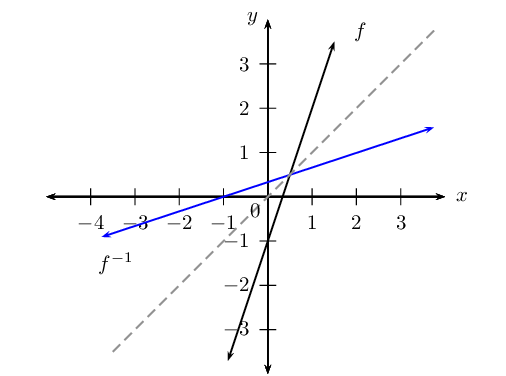

$T\left( \frac{4}{3}; 3 \right)$ is a point on $f$ and $R$ is a point on $f^{-1}$. Determine the coordinates of $R$ if $R$ and $T$ are symmetrical.

$R\left( 3; \frac{4}{3} \right)$

Explain why the line $y = x$ is an axis of symmetry for a function and its inverse.

To reflect a function about the $y$-axis, we replace every $x$ with $-x$. Similarly, to reflect a function about the $x$-axis, we replace every $y$ with $-y$. To reflect a function about the line $y=x$, we replace $x$ with $y$ and $y$ with $x$, which is how we determine the inverse.

Will the line $y = -x$ be an axis of symmetry for a function and its inverse?

No it will not.

Given ${f}^{-1}\left(x\right)=-2x+4$, determine $f\left(x\right)$.

\begin{align*} f^{-1}(x): y & = -2x + 4 \\ f(x): x & = -2y + 4 \\ \therefore 2y & = -x + 4 \\ y & = -\frac{1}{2}x + 2\\ \therefore f(x) & = -\frac{1}{2}x + 2 \end{align*}

Calculate the intercepts of $f(x)$ and $f^{-1}(x)$.

Consider $f(x)$:

\begin{align*} \text{Let } y & = -\frac{1}{2}x + 2 \\ \text{Let } x=0: \quad y & = -\frac{1}{2}(0) + 2 \\ y & = 2 \\ \therefore y &-\text{intercept is } (0;2) \\ & \\ \text{Let } y=0: \quad 0 & = -\frac{1}{2}x + 2 \\ -2 & = -\frac{1}{2}x \\ x & = 4 \\ \therefore x &-\text{intercept is } (4;0) \end{align*}

Consider $f^{-1}(x)$:

\begin{align*} \text{Let } y & = - 2x+4 \\ \text{Let } x=0: \quad y & = - 2(0) + 4\\ y & = 4 \\ \therefore y &-\text{intercept is } (0;4) \\ & \\ \text{Let } y=0: \quad 0 & = - 2x+4\\ 2x & = 4 \\ x & = 2 \\ \therefore x &-\text{intercept is } (2;0) \end{align*}

Therefore the intercepts for $f(x)$ are $(4;0)$ and $(0;2)$ and the intercepts for $f^{-1}(x)$ are $(2;0)$ and $(0;4)$.

Determine the coordinates of $T$, the point of intersection of $f(x)$ and $f^{-1}(x)$.

To find the point on intersection, we let $f(x) = f^{-1}(x)$:

\begin{align*} -\frac{1}{2}x + 2 & = -2x + 4 \\ -\frac{1}{2}x + 2x & = 4 - 2 \\ \frac{3}{2}x & = 2 \\ \therefore x & = \frac{4}{3} \\ \text{And } y & = -2 \left( \frac{4}{3} \right) + 4 \\ & = - \frac{8}{3} + 4 \\ & = \frac{4}{3} \end{align*}

This gives the point $T \left( \frac{4}{3};\frac{4}{3} \right)$.

Sketch the graphs of $f$ and $f^{-1}$ on the same system of axes. Indicate the intercepts and point $T$ on the graph.