8.4 Triangles (EMCJB)

Proportionality of triangles (EMCJC)

In the diagram below, $\triangle ABC$ and $\triangle DEF$ have the same height $(h)$ since both triangles are between the same parallel lines.

Triangles with equal heights have areas which are proportional to their bases.
$\triangle WXY$ and $\triangle ZXY$ have the same base $(XY)$ and the same height $(h)$ since both triangles lie between the same parallel lines.

Triangles with equal bases and between the same parallel lines are equal in area.
$\triangle PQR$ and $\triangle SQR$ have the same base $(QR)$ and are equal in area.

Triangles on the same side of the same base and equal in area, lie between parallel lines.

Worked example 2: Proportionality of triangles

Given parallelogram $PQRS$ with $QR$ produced to $T$ . $RS = \text{45}\text{ cm}$ , $QR = \text{30}\text{ cm}$ and $h = \text{10}\text{ cm}$ .

Calculate $H$ .
If $TR:TQ = 1:4$ , show that $\frac{\text{Area } \triangle STR}{\text{Area } \triangle PRQ} = \frac{1}{3}$ .

Determine the length of $H$

We use the formula for area of a parallelogram to calculate $H$ .

$\begin{align*} \text{Area } PQRS &= SR \times h \\ &= 45 \times 10 \\ &= \text{450}\text{ cm$^{2}$} \\ & \\ \text{Area } PQRS &= QR \times H \\ 450 &= 30 \times H \\ \therefore H &= \text{15}\text{ cm} \end{align*}$

Use proportionality to show that $\frac{\text{Area } \triangle STR}{\text{Area } \triangle PRQ} = \frac{1}{3}$

We are given the ratio $TR:TQ = 1:4$ .

$\begin{align*} \frac{TR}{TQ} &= \frac{1}{4} \\ \text{So then } \frac{RQ}{TQ} &= \frac{3}{4} \\ \text{And } \frac{TR}{RQ} &= \frac{TR}{TQ} \times \frac{TQ}{RQ} \\ &= \frac{1}{4} \times \frac{4}{3} \\ &= \frac{1}{3} \end{align*}$

$\begin{align*} \text{Area } \triangle STR &= \frac{1}{2} TR \times H \quad (PS \parallel QT, \text{ equal heights}) \\ \text{Area } \triangle PRQ &= \frac{1}{2} RQ \times H \\ & \\ \therefore \frac{\text{Area } \triangle STR}{\text{Area } \triangle PRQ} &= \frac{\frac{1}{2} TR \times H}{\frac{1}{2} RQ \times H} \\ &= \frac{TR}{RQ} \\ &= \frac{1}{3} \end{align*}$

Proportionality of triangles

Textbook Exercise 8.4

$\frac{BC}{AB}$

We are given that $ED: DC = 4:6$, which we can write as a fraction and simplify:

\begin{align*} \frac{ED}{DC} &= \frac{4}{6} \\ &= \frac{2}{3} \\ & \\ \text{And } \frac{ED}{DC} &= \frac{AB}{BC} \\ \frac{AB}{BC} &= \frac{2}{3} \\ \therefore \frac{BC}{AB} &= \frac{3}{2} \end{align*}

$AB:AC$

\begin{align*} \frac{AB}{AC} &= \frac{ED}{EC} \\ &= \frac{2}{2 + 3} \\ &= \frac{2}{5} \end{align*}

The lengths of $AC$ and $ED$, if it is given that $AB = \text{12}\text{ mm}$.

\begin{align*} \frac{AB}{AC} &= \frac{ED}{EC} \\ &= \frac{2}{2 + 3} \\ &= \frac{2}{5} \\ \text{And we know } AB &= \text{12}\text{ mm} \\ \frac{AB}{AC} &= \frac{2}{5} \times \frac{6}{6} \\ &= \frac{12}{30} \\ \therefore AC &= \text{30}\text{ mm} \end{align*}

We cannot determine the length of $ED$ since we do not know the lengths of $DC$, or $EC$. We only know that $\frac{ED}{EC} = \frac{2}{5}$.

In right-angled $\triangle MNP$, $QR$ is drawn parallel to $NM$, with $R$ the mid-point of $MP$. $NP = \text{16}\text{ cm}$ and $RQ = \text{60}\text{ mm}$. Determine $QP$ and $RP$.

\begin{align*} \frac{RP}{MP} &= \frac{QP}{NP} \\ &= \frac{1}{2} \\ \therefore \frac{QP}{16} &= \frac{1}{2} \\ \therefore QP &= \text{8}\text{ cm} \end{align*}

Use the theorem of Pythagoras to determine $RP$.

\begin{align*} \text{In } \triangle RQP: \quad PR^{2} &= QR^{2} + QP^{2} \\ &= (8)^{2} + (6)^{2} \\ &= 64 + 36 \\ &= 100 \\ \therefore PR &= \text{10}\text{ cm} \end{align*}

Prove that $BD$ bisects $\hat{D}$.

\[\begin{array}{rll} A\hat{D}B &= A\hat{B}D & (AD = AB) \\ A\hat{B}D &= B\hat{D}C & (AB \parallel DC, \text{ alt. } \angle \text{s}) \\ \therefore A\hat{D}B &= B\hat{D}C & \\ \therefore BD & \text{ bisects } \hat{D} & \end{array}\]

Prove that the two diagonals are equal in length.

\[\begin{array}{rll} AD &= BC & (\text{given}) \\ A\hat{D}C &= B\hat{C}D & (\text{given}) \\ DC &= DC & \\ \therefore \triangle ADC &\equiv \triangle BCD & (\text{SAS}) \\ \therefore AC &= BD & \end{array}\]

If $DC:AB = 5:4$, show that area $ABCD = \text{2,25} \times \text{ area } \triangle ABC$.

\[\begin{array}{rll} \frac{DC}{AB} &= \frac{5}{4} & (\text{given}) \\ & & \\ \therefore \dfrac{\text{Area } \triangle BDC}{\text{Area } \triangle BDA} &= \frac{5}{4} & (\text{same height, } DC \parallel AB ) \\ & & \\ \therefore \dfrac{\text{Area } ABCD}{\text{Area } \triangle BDA} &= \frac{9}{4} & \\ & & \\ \text{And } \triangle BDA &= \triangle ABC & (\text{same height, same base }AB) \\ & & \\ \therefore \dfrac{\text{Area } ABCD}{\text{Area } \triangle ABC} &= \text{2,25} & \\ & & \\ \text{Area } ABCD &= \text{2,25} \left( \text{Area } \triangle ABC \right) & \end{array}\]

In the diagram below, $\triangle PQR$ is given with $QR \parallel TS$.

Show that area $\triangle PQS = \text{ area } \triangle PRT$.

\[\begin{array}{rll} \text{Area } \triangle PQS &= \text{Area } \triangle PTS + \text{Area } \triangle SQT & \\ \text{Area } \triangle PRT &= \text{Area } \triangle PTS + \text{Area } \triangle SRT & \\ \text{Consider } \triangle SQT &\text{ and } \triangle SRT & \\ ST &\text{ is common base } & \\ QR \parallel TS, & \text{ therefore same height } & \\ \therefore \text{Area } \triangle SQT &= \text{Area } \triangle SRT & \\ \therefore \text{Area } \triangle PQS &= \text{Area } \triangle PRT & \end{array}\]

Complete the following statement of the mid-point theorem:

"The line joining $\ldots \ldots$ of a triangle is $\ldots \ldots$ to the third side and equal to $\ldots \ldots$"

"The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side."

In $\triangle PQR$, $T$ and $S$ are the mid-points of $PR$ and $PQ$ respectively. Prove $TS \parallel RQ$.

Hint: make a construction by drawing $SR$ and $TQ$.

Write down the converse of the mid-point theorem.

Converse: a line through the mid-point of one side of a triangle, parallel to a second side, bisects the third side.

Chapter 8: Theorem: Proportion theorem

A line drawn parallel to one side of a triangle divides the other two sides of the triangle in the same proportion.

(Reason: line $\parallel$ to one side $\triangle$ )

$\triangle ABC$ with line $DE\parallel BC$

$\frac{AD}{DB}=\frac{AE}{EC}$

Draw ${h}_{1}$ from $E$ perpendicular to $AD$ , and ${h}_{2}$ from $D$ perpendicular to $AE$ .

Draw $BE$ and $CD$ .

$\begin{align*} \dfrac{\text{Area }\triangle ADE}{\text{Area }\triangle BDE} & = \dfrac{\frac{1}{2}AD.{h}_{1}}{\frac{1}{2}DB.{h}_{1}}=\dfrac{AD}{DB} \\ & \\ \dfrac{\text{Area }\triangle ADE}{\text{Area }\triangle CED} & = \dfrac{\frac{1}{2}AE.{h}_{2}}{\frac{1}{2}EC.{h}_{2}}=\dfrac{AE}{EC} \\ & \\ \text{but} \enspace \text{Area }\triangle BDE & = \text{Area }\triangle CED \quad \text{(equal }\text{base }\text{and }\text{height)} \\ & \\ \therefore \frac{\text{Area }\triangle ADE}{\text{Area }\triangle BDE} & = \frac{\text{Area }\triangle ADE}{\text{Area }\triangle CED} \\ & \\ \therefore \frac{AD}{DB} & = \frac{AE}{EC} \end{align*}$

Similarly, we use the same method to show that:

$\frac{AD}{AB} = \frac{AE}{AC} \quad \text{ and } \quad \frac{AB}{BD} = \frac{AC}{CE}$

Converse: proportion theorem

If a line divides two sides of a triangle in the same proportion, then the line is parallel to the third side.

(Reason: line divides sides in prop.)

Worked example 3: Proportion theorem

In $\triangle TQP$ , $SR \parallel QP$ , $SQ = \text{12}\text{ cm}$ and $RP = \text{15}\text{ cm}$ . If $TR = \frac{x}{3}$ , $TP = x$ and $TS = y$ , determine the values of $x$ and $y$ , giving reasons.

Use the proportion theorem to determine the values of $x$ and $y$

Consider $TP$ :

$\begin{array}{rll} RP & = x - \frac{1}{3}x& \\ & & \\ & = \frac{2}{3}x &\\ & & \\ \therefore 15 & = \frac{2}{3}x& \\ & & \\ x & = \text{22,5}\text{ cm} & \\ & &\\ TR & = \frac{1}{3}(\text{22,5})& \\ & & \\ & = \text{7,5}\text{ cm} & \end{array}$

Consider $TQ$ :

$\begin{array}{rll} \frac{TS}{SQ} & = \frac{TR}{RP} & (\text{line } \parallel \text{ one side of } \triangle) \\ & & \\ \frac{y}{12} & = \frac{\text{7,5}}{15} & \\ & & \\ \therefore y & = \text{6}\text{ cm} & \end{array}$

Special case: the mid-point theorem

A corollary of the proportion theorem is the mid-point theorem: the line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.

If $AB = BD$ and $AC = CE$ , then $BC \parallel DE$ and $BC = \frac{1}{2}DE$ .

We also know that $\frac{AC}{CE} = \frac{AB}{BD}$ .

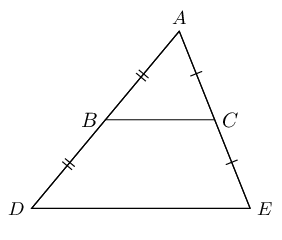
Converse: the mid-point theorem

The line drawn from the mid-point of one side of a triangle parallel to another side, bisects the third side of the triangle.

If $AB = BD$ and $BC \parallel DE$ , then $AC = CE$ .

Proportion theorem

Textbook Exercise 8.5

Calculate $JP:NP$.

\[\begin{array}{rll} \dfrac{JP}{NP}&= \dfrac{HM}{NM} & (HJ \parallel MP) \\ &= \frac{x}{x + 3x} & \\ &= \frac{x}{4x} & \\ &= \frac{1}{4} & \end{array}\]

Calculate $\dfrac{\text{area } \triangle HNJ}{\text{area } \triangle MNP}$.

\[\begin{array}{rll} \dfrac{HN}{MH} &= \dfrac{3}{1} & \\ \therefore HN &= 3x & \\ NJ &= 3y & \\ & & \\ \text{In } \triangle HNJ: \quad H&= \text{90}° & (HJ \parallel MP) \\ \therefore HJ^{2} &= NJ^{2} - NH^{2} & \\ &= (3y)^{2} - (3x)^{2} & \\ &= 9y^{2} - 9x^{2} & \\ HJ &= \sqrt{9(y^{2}-x^{2})} & \\ &= 3 \sqrt{y^{2} - x^{2}} & \\ \end{array}\] \[\begin{array}{rll} \text{In } \triangle MNP: \quad \hat{M} &= \text{90}° & \\ MP^{2} &= (4y)^{2} - (4x)^{2} & \\ MP &= \sqrt{16(y^{2}-x^{2})} & \\ MP &= 4 \sqrt{y^{2}-x^{2}} & \\ & & \\ \dfrac{\text{area } \triangle HNJ}{\text{area } \triangle MNP} &= \dfrac{\frac{1}{2} HJ \times HN}{\frac{1}{2} MP \times MN} & \\ &= \dfrac{3 \sqrt{y^{2}-x^{2}} \times 3x}{4 \sqrt{y^{2}-x^{2}} \times 4x} & \\ &= \frac{9}{16} & \end{array}\]

Use the given diagram to prove the Proportion Theorem.

Given: $AB \parallel CD$

Required to prove: $AE:ED = BE:EC$

Construction: Draw $AC$ and $BD$

Proof: use area of $\triangle$'s

\[\begin{array}{rll} \dfrac{\triangle AEB}{\triangle ACB}&= \dfrac{EB}{CB} & (\text{same height}) \\ \dfrac{\triangle AEB}{\triangle ADB}&= \dfrac{AE}{AD} & (\text{same height}) \\ \text{But } \quad \triangle ACB &= \triangle ADB & (AB \parallel CD \enspace \therefore \text{ same height}) \\ \therefore \dfrac{EB}{CB} &= \dfrac{EA}{DA} & \\ \therefore \dfrac{EB}{CE} &= \dfrac{EA}{DE} & \end{array}\]

In the diagram below, $JL = 2, LI = y, IM =7 \text{ and } MK = y - 2.$

If $LM \parallel JK$, calculate $y$ (correct to two decimal places).

\[\begin{array}{rll} \frac{LI}{JL} &= \frac{MI}{KM} & (LM \parallel JK) \\ \frac{y}{2} &= \frac{7}{y-2} & \\ y (y-2) &= 14 & \\ y^{2}-2y-14 &= 0 & \\ y &= \dfrac{-(-2)±\sqrt{4-4(-14)}}{2} & \\ &= \dfrac{2±\sqrt{60}}{2} & \\ y &= \text{4,87} \text{ or } -\text{2,87} & \\ \text{But } y & > 0 & \\ \therefore y &= \text{4,87} & \end{array}\]

Write down the converse of the proportion theorem and illustrate with a diagram.

Converse of the proportion theorem: a line cutting two sides of a triangle proportionally will be parallel to the third side.

Prove that $YBMN$ is a parallelogram.

Consider $\triangle ABX:$

\[\begin{array}{rll} YN &\parallel BX & (Y \text{ and } N \text{ mid-points of } AB \text { and } AX ) \\ MN &\parallel BA & (M \text{ and } N \text{ mid-points of } BX \text { and } XA ) \\ \therefore YBMN &\text{ is a parallelogram} & (\text{both opp. sides } \parallel) \end{array}\]

Prove that $MR = \frac{1}{2}BC$.

Consider $\triangle AXC:$

\[\begin{array}{rll} RN &\parallel CA & (\text{given}) \\ \text{And } XN &= NA & (N \text{ mid-point of } AB ) \\ \therefore XR &= RC & \\ M &\text{ is the mid-point } BX & (\text{given}) \\ \therefore MX + XR &= \frac{1}{2}BX + \frac{1}{2}XC & \\ \therefore MR &= \frac{1}{2}(BX + XC) & \\ MR &= \frac{1}{2}(BC) & \end{array}\]

8.3 Polygons

Table of Contents

8.5 Similarity