\(5; 20; 45; 80; \ldots\)
3.2 Quadratic sequences
|
Previous
3.1 Revision
|
Next
3.3 Summary
|
3.2 Quadratic sequences (EMBG5)
Quadratic sequences
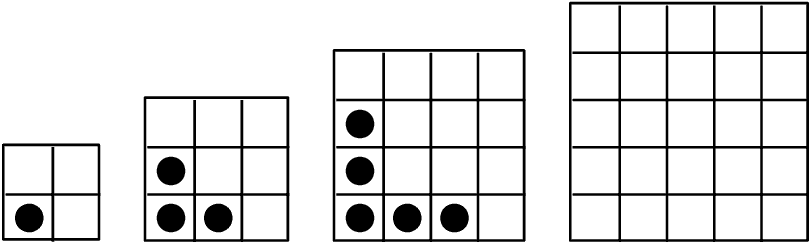
- Study the dotted-tile pattern shown and answer the following questions.
- Complete the fourth pattern in the diagram.
-
Complete the table below:
pattern number 1 2 3 4 5 20 n dotted tiles 1 3 5 difference (d) − 2 - What do you notice about the change in number of dotted tiles?
- Describe the pattern in words: “The number of dotted tiles...”.
- Write the general term: Tn=…
- Give the mathematical name for this kind of pattern.
- A pattern has 819 dotted tiles. Determine the value of n.
- Now study the number of blank tiles (tiles without dots) and answer the following questions:
-
Complete the table below:
pattern number 1 2 3 4 5 10 blank tiles 3 6 11 first difference − 3 second difference − − - What do you notice about the change in the number of blank tiles?
- Describe the pattern in words: “The number of blank tiles...”.
- Write the general term: Tn=…
- Give the mathematical name for this kind of pattern.
- A pattern has 227 blank tiles. Determine the value of n.
- A pattern has 79 dotted tiles. Determine the number of blank tiles.
-
- Quadratic sequence
-
A quadratic sequence is a sequence of numbers in which the second difference between any two consecutive terms is constant.
Consider the following example: 1;2;4;7;11;…
The first difference is calculated by finding the difference between consecutive terms:
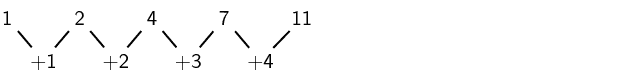
The second difference is obtained by taking the difference between consecutive first differences:
We notice that the second differences are all equal to 1. Any sequence that has a common second difference is a quadratic sequence.
It is important to note that the first differences of a quadratic sequence form a sequence. This sequence has a constant difference between consecutive terms. In other words, a linear sequence results from taking the first differences of a quadratic sequence.
General case
If the sequence is quadratic, the nth term is of the form Tn=an2+bn+c.

In each case, the common second difference is a 2a.
Quadratic sequences
Determine the second difference between the terms for the following sequences:
\(6; 11; 18; 27; \ldots\)
\(1; 4; 9; 16; \ldots\)
\(3; 0; -5; -12; \ldots\)
\(1; 3; 7; 13; \ldots\)
\(0; -6; -16; -30; \ldots\)
\(-1; 2; 9; 20; \ldots\)
\(1; -3; -9; -17; \ldots\)
\(3a+1; 12a+1; 27a+1; 48a+1 \ldots\)
\(2; 10; 24; 44; \ldots\)
\(t-2; 4t-1; 9t; 16t+1; \ldots\)
Complete the sequence by filling in the missing term:
\(11; 21; 35; \ldots; 75\)
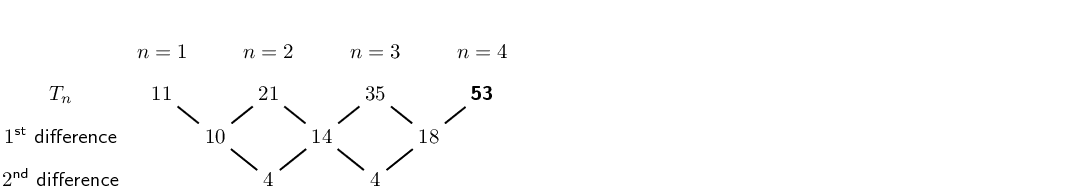
\(20; \ldots; 42; 56; 72\)
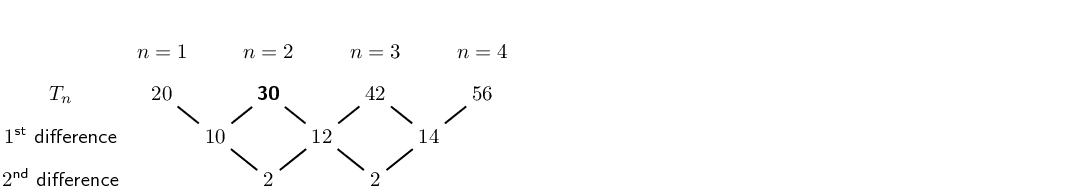
\(\ldots; 37; 65; 101\)
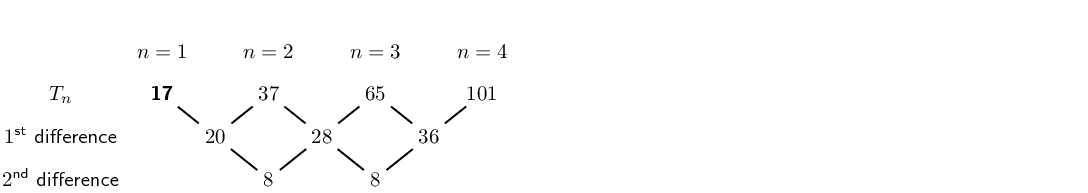
\(3; \ldots; -13; -27; -45\)
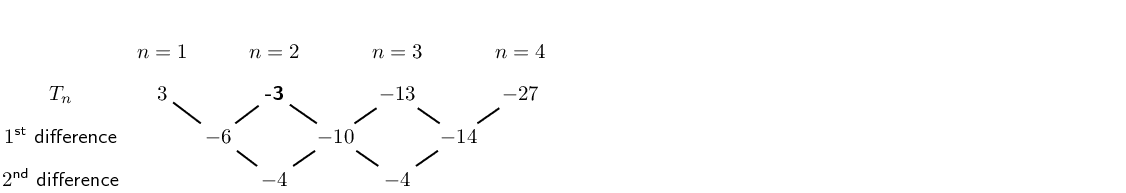
\(24; 35; 48; \ldots; 80\)
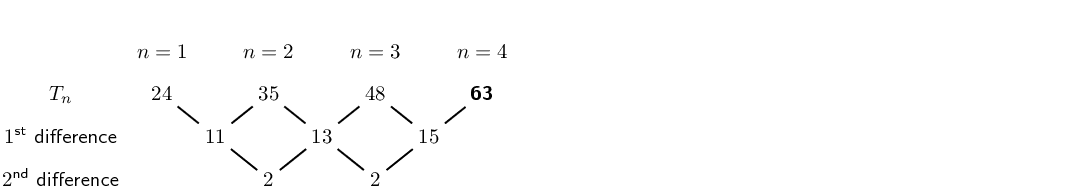
\(\ldots; 11; 26; 47\)
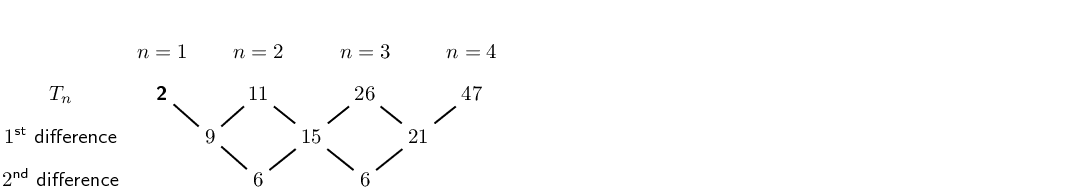
Use the general term to generate the first four terms in each sequence:
\(T_n = n^2+3n-1\)
\(T_n = -n^2-5\)
\(T_n = 3n^2-2n\)
\(T_n = -2n^2+n+1\)
Worked example 2: Quadratic sequences
Write down the next two terms and determine an equation for the nth term of the sequence 5; 12; 23; 38; …
Find the first differences between the terms
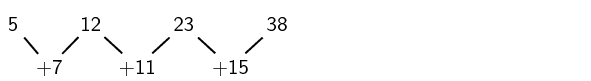
Find the second differences between the terms
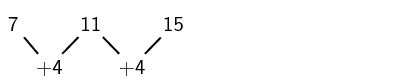
So there is a common second difference of 4. We can therefore conclude that this is a quadratic sequence of the form Tn=an2+bn+c.
Continuing the sequence, the next first differences will be:
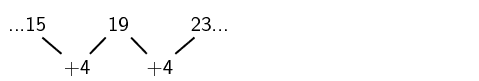
Finding the next two terms in the sequence
The next two terms will be:
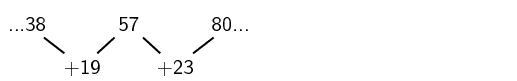
So the sequence will be: 5; 12; 23; 38; 57; 80; …
Determine the general term for the sequence
To find the values of a, b and c for Tn=an2+bn+c we look at the first 3 terms in the sequence:
n=1:T1=a+b+cn=2:T2=4a+2b+cn=3:T3=9a+3b+cWe solve a set of simultaneous equations to determine the values of a, b and c
We know that T1=5, T2=12 and T3=23
a+b+c=54a+2b+c=129a+3b+c=23T2−T1=4a+2b+c−(a+b+c)12−5=4a+2b+c−a−b−c7=3a+b…(1)T3−T2=9a+3b+c−(4a+2b+c)23−12=9a+3b+c−4a−2b−c11=5a+b…(2)(2)−(1)=5a+b−(3a+b)11−7=5a+b−3a−b4=2a∴a=2Using equation (1):3(2)+b=7∴b=1And using a+b+c=52+1+c=5∴c=1Write the general term for the sequence
Tn=2n2+n+2
Worked example 3: Plotting a graph of terms in a sequence
Consider the following sequence:
3;6;10;15;21;…
- Determine the general term (Tn) for the sequence.
- Is this a linear or a quadratic sequence?
- Plot a graph of Tn vs n.
Determine the first and second differences
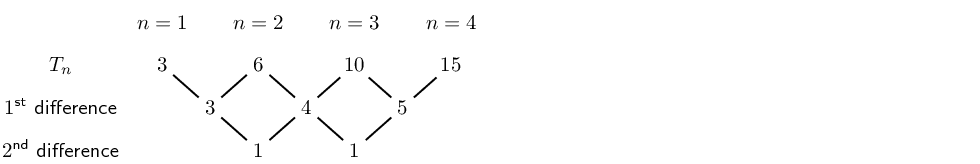
We see that the first differences are not constant and form the sequence 3;4;5;… and that there is a common second difference of 1. Therefore the sequence is quadratic and has a general term of the form Tn=an2+bn+c.
Determine the general term Tn
To find the values of a, b and c for Tn=an2+bn+c we look at the first 3 terms in the sequence:
n=1:T1=a+b+cn=2:T2=4a+2b+cn=3:T3=9a+3b+cWe solve this set of simultaneous equations to determine the values of a, b and c. We know that T1=3, T2=6 and T3=10.
a+b+c=34a+2b+c=69a+3b+c=10T2−T1=4a+2b+c−(a+b+c)6−3=4a+2b+c−a−b−c3=3a+b…(1)T3−T2=9a+3b+c−(4a+2b+c)10−6=9a+3b+c−4a−2b−c4=5a+b…(2)(2)−(1)=5a+b−(3a+b)4−3=5a+b−3a−b1=2a∴a=12Using equation (1):3(12)+b=3∴b=32And using a+b+c=312+32+c=3∴c=1Therefore the general term for the sequence is Tn=12n2+32n+1.
Plot a graph of Tn vs n
Use the general term for the sequence, Tn=12n2+32n+1, to complete the table.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Tn | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 |
Use the table to plot the graph:
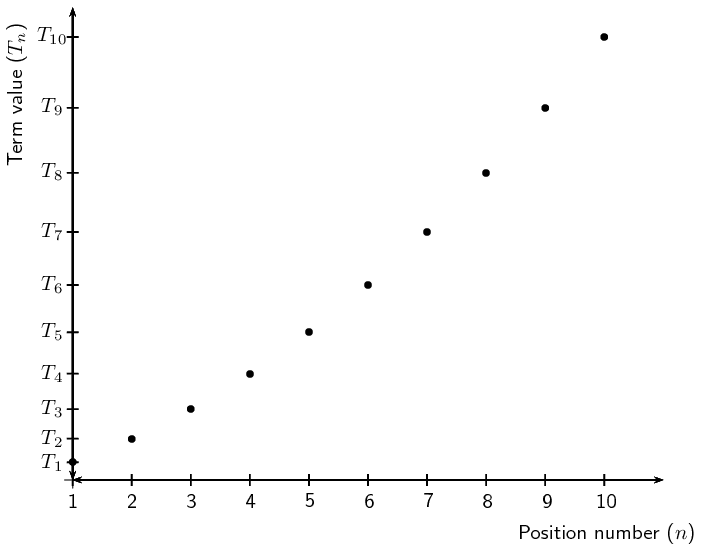
In this case it would not be accurate to join these points, since n indicates the position of a term in a sequence and can therefore only be a positive integer. We can, however, see that the plot of the points lies in the shape of a parabola.
Worked example 4: Olympic Games soccer event
In the first stage of the soccer event at the Olympic Games, there are teams from four different countries in each group. Each country in a group must play every other country in the group once.
- How many matches will be played in each group in the first stage of the event?
- How many matches would be played if there are 5 teams in each group?
- How many matches would be played if there are 6 teams in each group?
- Determine the general formula of the sequence.
Determine the number of matches played if there are 4 teams in a group
Let the teams from four different countries be A, B, C and D.
| teams in a group | matches played |
| A | AB,AC,AD |
| B | BC,BD |
| C | CD |
| D | |
| 4 | 3+2+1=6 |
AB means that team A plays team B and BA would be the same match as AB. So if there are four different teams in a group, each group plays 6 matches.
Determine the number of matches played if there are 5 teams in a group
Let the teams from five different countries be A,B,C,D and E.
| teams in a group | matches played |
| A | AB,AC,AD,AE |
| B | BC,BD,BE |
| C | CD,CE |
| D | DE |
| E | |
| 5 | 4+3+2+1=10 |
So if there are five different teams in a group, each group plays 10 matches.
Determine the number of matches played if there are 6 teams in a group
Let the teams from six different countries be A,B,C,D,E and F.
| teams in a group | matches to be played |
| A | AB,AC,AD,AE,AF |
| B | BC,BD,BE,BF |
| C | CD,CE,CF |
| D | DE,DF |
| E | EF |
| F | |
| 5 | 5+4+3+2+1=15 |
So if there are six different teams in a group, each group plays 15 matches.
We continue to increase the number of teams in a group and find that a group of 7 teams plays 21 matches and a group of 8 teams plays 28 matches.
Consider the sequence
We examine the sequence to determine if it is linear or quadratic:
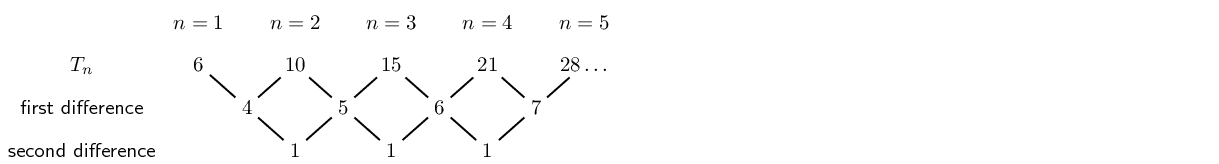
We see that the first differences are not constant and that there is a common second difference of 1. Therefore the sequence is quadratic and has a general term of the form Tn=an2+bn+c.
Determine the general term Tn
To find the values of a, b and c for Tn=an2+bn+c we look at the first 3 terms in the sequence:
n=1:T1=a+b+cn=2:T2=4a+2b+cn=3:T3=9a+3b+cWe solve a set of simultaneous equations to determine the values of a, b and c. We know that T1=6, T2=10 and T3=15
a+b+c=64a+2b+c=109a+3b+c=15T2−T1=4a+2b+c−(a+b+c)10−6=4a+2b+c−a−b−c4=3a+b…(1)T3−T2=9a+3b+c−(4a+2b+c)15−10=9a+3b+c−4a−2b−c5=5a+b…(2)(2)−(1)=5a+b−(3a+b)5−4=5a+b−3a−b1=2a∴a=12Using equation (1):3(12)+b=4∴b=52And using a+b+c=612+52+c=6∴c=3Therefore the general term for the sequence is Tn=12n2+52n+3.
Quadratic sequences
Calculate the common second difference for each of the following quadratic sequences:
\(3; \; 6; \; 10; \; 21; \; ...\)
\(4; \; 9; \; 16; \; 25; \; ...\)
\(7; \; 17; \; 31; \; 49; \; ...\)
\(2; \; 10; \; 26; \; 50; \; 82 ...\)
\(31; \; 30; \; 27; \; 22; \; 15; \; ...\)
Find the first five terms of the quadratic sequence defined by: \(T_n = 5n^2 + 3n + 4\).
Given \(T_n = 4n^2 + 5n + 10\), find \(T_9\).
Given \(T_n = 2n^2\), for which value of \(n\) does \(T_n = 32\)?
Write down the next two terms of the quadratic sequence: \(16; 27; 42; 61; \ldots\)
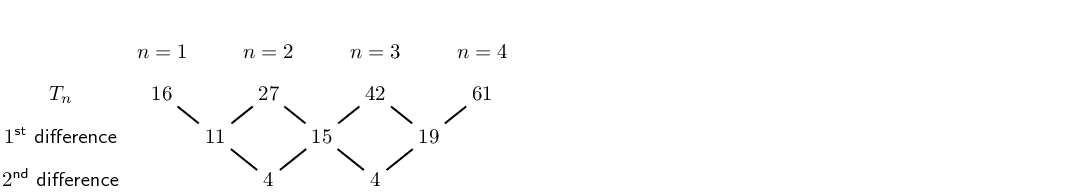
Find the general formula for the quadratic sequence above.
|
Previous
3.1 Revision
|
Table of Contents |
Next
3.3 Summary
|
