\(y_1 = \cos \theta\)
5.6 The cosine function
|
Previous
5.5 The sine function
|
Next
5.7 The tangent function
|
5.6 The cosine function (EMBH3)
Revision (EMBH4)
Functions of the form \(y = \cos \theta\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
-
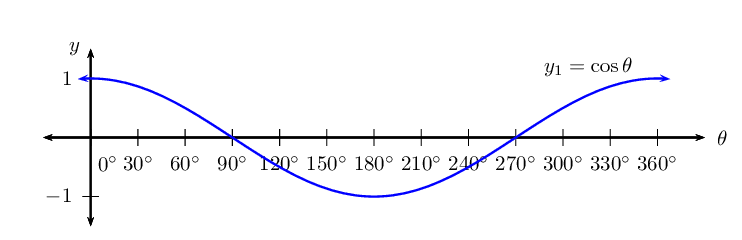
The period is \(\text{360}\text{°}\) and the amplitude is \(\text{1}\).
-
Domain: \([\text{0}\text{°};\text{360}\text{°}]\)
For \(y = \cos \theta\), the domain is \(\{ \theta: \theta \in \mathbb{R} \}\), however in this case, the domain has been restricted to the interval \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
-
Range: \(\left[-1;1\right]\)
-
\(x\)-intercepts: \(\left(\text{90}\text{°};0\right)\), \(\left(\text{270}\text{°};0\right)\)
-
\(y\)-intercept: \(\left(\text{0}\text{°};1\right)\)
-
Maximum turning points: \(\left(\text{0}\text{°};1\right)\), \(\left(\text{360}\text{°};1\right)\)
-
Minimum turning point: \(\left(\text{180}\text{°};-1\right)\)
Functions of the form \(y = a \cos \theta + q\)
Cosine functions of the general form \(y = a \cos \theta + q\), where \(a\) and \(q\) are constants.
The effects of \(a\) and \(q\) on \(f(\theta) = a \cos \theta + q\):
-
The effect of \(q\) on vertical shift
-
For \(q>0\), \(f(\theta)\) is shifted vertically upwards by \(q\) units.
-
For \(q<0\), \(f(\theta)\) is shifted vertically downwards by \(q\) units.
-
-
The effect of \(a\) on shape
-
For \(a>1\), the amplitude of \(f(\theta)\) increases.
-
For \(0<a<1\), the amplitude of \(f(\theta)\) decreases.
-
For \(a<0\), there is a reflection about the \(x\)-axis.
-
For \(-1 < a < 0\), there is a reflection about the \(x\)-axis and the amplitude decreases.
-
For \(a < -1\), there is a reflection about the \(x\)-axis and the amplitude increases.
-
Revision
Textbook Exercise
5.24
On separate axes, accurately draw each of the following functions for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\):
- Use tables of values if necessary.
- Use graph paper if available.
For each function in the previous problem determine the following:
- Period
- Amplitude
- Domain and range
- \(x\)- and \(y\)-intercepts
- Maximum and minimum turning points
\(y_2 = - 3 \cos \theta\)
\(y_3 = \cos \theta + 2\)
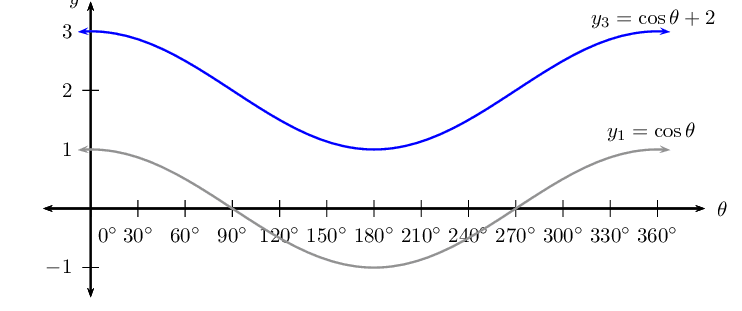
\(y_4 = \frac{1}{2} \cos \theta - 1\)
Functions of the form \(y=\cos (k\theta)\) (EMBH5)
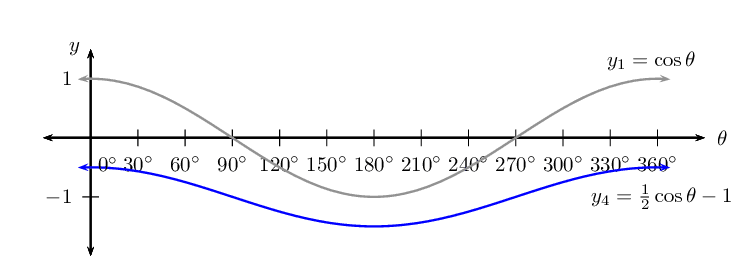
We now consider cosine functions of the form \(y = \cos k\theta\) and the effects of parameter \(k\).
The effects of \(k\) on a cosine graph
- Complete the following table for \(y_1 = \cos \theta\) for
\(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\):
θ \(-\text{360}\)\(\text{°}\) \(-\text{300}\)\(\text{°}\) \(-\text{240}\)\(\text{°}\) \(-\text{180}\)\(\text{°}\) \(-\text{120}\)\(\text{°}\) \(-\text{60}\)\(\text{°}\) \(\text{0}\)\(\text{°}\) \(\cos \theta\) θ \(\text{60}\)\(\text{°}\) \(\text{120}\)\(\text{°}\) \(\text{180}\)\(\text{°}\) \(\text{240}\)\(\text{°}\) \(\text{300}\)\(\text{°}\) \(\text{360}\)\(\text{°}\) \(\cos \theta\) -
Use the table of values to plot the graph of \(y_1 = \cos \theta\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
-
On the same system of axes, plot the following graphs:
- \(y_2 = \cos (-\theta)\)
- \(y_3 = \cos 3\theta\)
- \(y_4 = \cos \frac{3\theta}{4}\)
-
Use your sketches of the functions above to complete the following table:
\(y_1\) \(y_2\) \(y_3\) \(y_4\) period amplitude domain range maximum turning points minimum turning points \(y\)-intercept(s) \(x\)-intercept(s) effect of \(k\) -
What do you notice about \(y_1 = \cos \theta\) and \(y_2 = \cos (-\theta)\)?
-
Is \(\cos (-\theta) = -\cos \theta\) a true statement? Explain your answer.
- Can you deduce a formula for determining the period of \(y = \cos k\theta\)?
The effect of the parameter \(k\) on \(y = \cos k\theta\)
The value of \(k\) affects the period of the cosine function.
-
For \(k > 0\):
For \(k > 1\), the period of the cosine function decreases.
For \(0 < k < 1\), the period of the cosine function increases.
-
For \(k < 0\):
For \(-1 < k < 0\), the period increases.
For \(k < -1\), the period decreases.
Negative angles: \[\cos (-\theta) = \cos \theta\] Notice that for negative values of \(\theta\), the graph is not reflected about the \(x\)-axis.
Calculating the period:
To determine the period of \(y = \cos k\theta\) we use, \[\text{Period } = \frac{\text{360}\text{°}}{|k|}\] where \(|k|\) is the absolute value of \(k\).
|
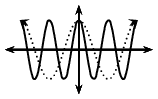
\(0 < k < 1\) |
\(-1 < k < 0\) |
 |
 |
|
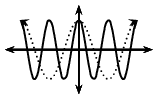
\(k > 1\) |
\(k < -1\) |
 |
 |
Worked example 22: Cosine function
- Sketch the following functions on the same set of axes for
\(-\text{180}\text{°} \leq \theta \leq
\text{180}\text{°}\).
- \(y_1 = \cos \theta\)
- \(y_2 = \cos \frac{\theta}{2}\)
-
For each function determine the following:
- Period
- Amplitude
- Domain and range
- \(x\)- and \(y\)-intercepts
- Maximum and minimum turning points
Examine the equations of the form \(y = \cos k\theta\)
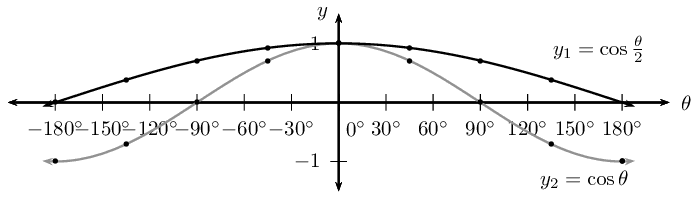
Notice that for \(y_2 = \cos \frac{\theta}{2}\), \(k < 1\) therefore the period of the graph increases.
Complete a table of values
| θ | \(-\text{180}\)\(\text{°}\) | \(-\text{135}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(-\text{45}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) |
| \(\cos \theta\) | \(-\text{1}\) | \(-\text{0,71}\) | \(\text{0}\) | \(\text{0,71}\) | \(\text{1}\) | \(\text{0,71}\) | \(\text{0}\) | \(-\text{0,71}\) | \(-\text{1}\) |
| \(\cos \frac{\theta}{2}\) | \(\text{0}\) | \(\text{0,38}\) | \(\text{0,71}\) | \(\text{0,92}\) | \(\text{1}\) | \(\text{0,92}\) | \(\text{0,71}\) | \(\text{0,38}\) | \(\text{0}\) |
Sketch the cosine graphs
Complete the table
| \(y_1 = \cos \theta\) | \(y_2 = \cos \frac{\theta}{2}\) | |
| period | \(\text{360}\text{°}\) | \(\text{720}\text{°}\) |
| amplitude | \(\text{1}\) | \(\text{1}\) |
| domain | \([-\text{180}\text{°};\text{180}\text{°}]\) | \([-\text{180}\text{°};\text{180}\text{°}]\) |
| range | \([-1;1]\) | \([0;1]\) |
| maximum turning points | \((\text{0}\text{°};1)\) | \((\text{0}\text{°};1)\) |
| minimum turning points | \((-\text{180}\text{°};-1) \text{ and } (\text{180}\text{°};-1)\) | none |
| \(y\)-intercept(s) | \((\text{0}\text{°};1)\) | \((\text{0}\text{°};1)\) |
| \(x\)-intercept(s) | \((-\text{90}\text{°};0) \text{ and } (\text{90}\text{°};0)\) | \((-\text{180}\text{°};0) \text{ and } (\text{180}\text{°};0)\) |
Discovering the characteristics
For functions of the general form: \(f(\theta) = y =\cos k\theta\):
Domain and range
The domain is \(\{ \theta: \theta \in \mathbb{R} \}\) because there is no value for \(\theta\) for which \(f(\theta)\) is undefined.
The range is \(\{ f(\theta): -1 \leq f(\theta) \leq 1, f(\theta) \in \mathbb{R} \}\) or \([-1;1]\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = \text{0}\text{°}\) and solving for \(f(\theta)\). \begin{align*} y &= \cos k\theta \\ &= \cos \text{0}\text{°} \\ &= 1 \end{align*} This gives the point \((\text{0}\text{°};1)\).
Cosine functions of the form \(y = \cos k\theta\)
Textbook Exercise 5.25
Sketch the following functions for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\). For each graph determine:
- Period
- Amplitude
- Domain and range
- \(x\)- and \(y\)-intercepts
- Maximum and minimum turning points
\(f(\theta) =\cos 2\theta\)
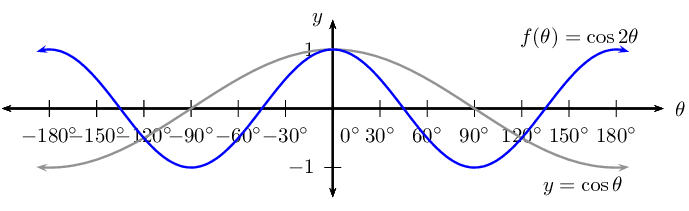
For \(f(\theta) =\cos 2 \theta\):
\begin{align*} \text{Period: } & \text{180}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{135}\text{°};0); (-\text{45}\text{°};0); (\text{45}\text{°};0); (\text{135}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};1) \\ \text{Max. turning point: } & (-\text{180}\text{°};1); (\text{0}\text{°};1); (\text{180}\text{°};1) \\ \text{Min. turning point: } & (-\text{90}\text{°};-1); (\text{90}\text{°};-1) \end{align*}\(g(\theta) =\cos \frac{\theta}{3}\)
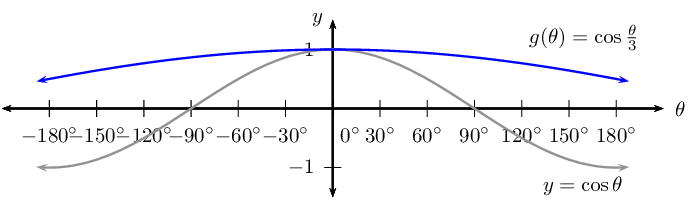
For \(g(\theta) =\cos \frac{\theta}{3}\):
\begin{align*} \text{Period: } & \text{1 080}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [\frac{1}{2};1] \\ x\text{-intercepts: } & \text{ none } \\ \text{Max. turning point: } & (\text{0}\text{°};1) \\ \text{Min. turning point: } & \text{ none } \end{align*}\(h(\theta) =\cos (-2\theta)\)
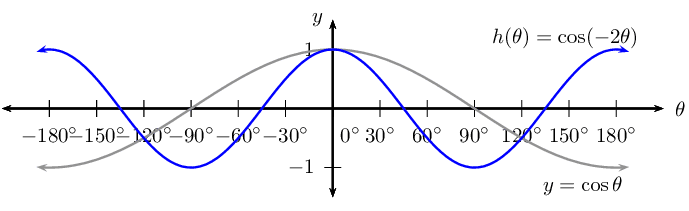
For \(h(\theta) =\cos (-2\theta)\):
\begin{align*} \text{Period: } & \text{180}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-1;1] \\ x\text{-intercepts: } & (-\text{135}\text{°};0); (-\text{45}\text{°};0); (\text{45}\text{°};0); (\text{135}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};1) \\ \text{Max. turning point: } & (-\text{180}\text{°};1); (\text{0}\text{°};1); (\text{180}\text{°};1) \\ \text{Min. turning point: } & (-\text{90}\text{°};-1); (\text{90}\text{°};-1) \end{align*}\(k(\theta) =\cos \frac{3\theta}{4}\)
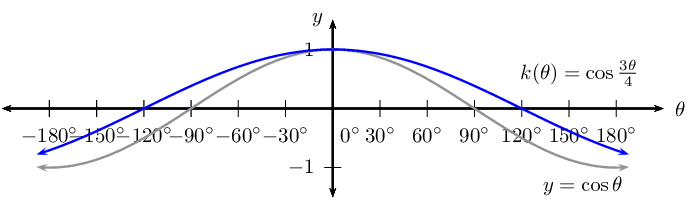
For \(k(\theta) =\cos \frac{3\theta}{4}\):
\begin{align*} \text{Period: } & \text{480}\text{°} \\ \text{Amplitude: } & 1 \\ \text{Domain: } & [-\text{180}\text{°};\text{180}\text{°}] \\ \text{Range: } & [-\frac{1}{\sqrt{2}};1] \\ x\text{-intercepts: } & (-\text{120}\text{°};0); (\text{120}\text{°};0) \\ y\text{-intercepts: } & (\text{0}\text{°};1) \\ \text{Max. turning point: } & (\text{0}\text{°};1) \\ \text{Min. turning point: } & \text{ none } \end{align*}For each graph of the form \(f(\theta) =\cos k\theta\), determine the value of \(k\):
\begin{align*}
\text{Period } &= \frac{\text{720}\text{°}}{3
\text{ complete waves }} \\
&= \text{240}\text{°} \\
\therefore \frac{\text{360}\text{°}}{k} &=
\text{240}\text{°} \\
\therefore k &=
\frac{\text{360}\text{°}}{\text{240}\text{°} }
\\
&= \frac{3}{2}
\end{align*}
\begin{align*}
\text{For } y &= \cos \theta \\
0 &= \cos \text{90}\text{°}\\
\text{So for } A(\text{135}\text{°};0) \qquad
\text{90}\text{°} &= k \times
\text{135}\text{°}\\
\therefore k &=
\frac{\text{90}\text{°}}{\text{135}\text{°} }
\\
&= \frac{2}{3}
\end{align*}
Functions of the form \(y=\cos\left(\theta +p\right)\) (EMBH6)
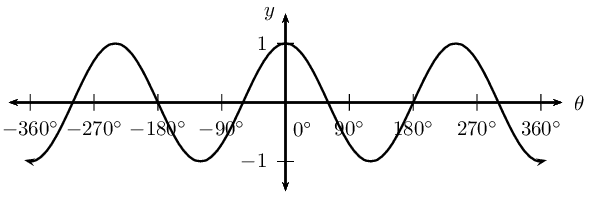
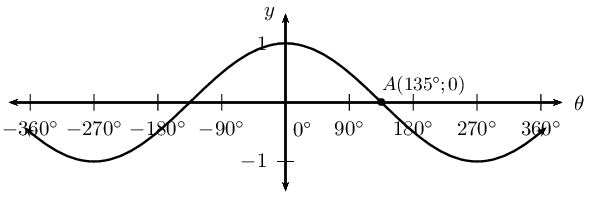
We now consider cosine functions of the form \(y = \cos(\theta + p)\) and the effects of parameter \(p\).
The effects of \(p\) on a cosine graph
-
On the same system of axes, plot the following graphs for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\):
- \(y_1 = \cos \theta\)
- \(y_2 = \cos (\theta - \text{90}\text{°})\)
- \(y_3 = \cos (\theta - \text{60}\text{°})\)
- \(y_4 = \cos (\theta + \text{90}\text{°})\)
- \(y_5 = \cos (\theta + \text{180}\text{°})\)
-
Use your sketches of the functions above to complete the following table:
\(y_1\) \(y_2\) \(y_3\) \(y_4\) \(y_5\) period amplitude domain range maximum turning points minimum turning points \(y\)-intercept(s) \(x\)-intercept(s) effect of \(p\)
The effect of the parameter on \(y = \cos(\theta + p)\)
The effect of \(p\) on the cosine function is a horizontal shift (or phase shift); the entire graph slides to the left or to the right.
-
For \(p > 0\), the graph of the cosine function shifts to the left by \(p\) degrees.
-
For \(p < 0\), the graph of the cosine function shifts to the right by \(p\) degrees.
|
\(p>0\) |
\(p<0\) |
 |
 |
Worked example 23: Cosine function
- Sketch the following functions on the same set of axes for
\(-\text{360}\text{°} \leq \theta \leq
\text{360}\text{°}\).
- \(y_1 = \cos \theta\)
- \(y_2 = \cos (\theta + \text{30}\text{°})\)
-
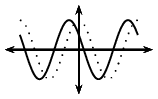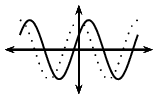For each function determine the following:
- Period
- Amplitude
- Domain and range
- \(x\)- and \(y\)-intercepts
- Maximum and minimum turning points
Examine the equations of the form \(y = \cos (\theta + p)\)
Notice that for \(y_1 = \cos \theta\) we have \(p = 0\) (no phase shift) and for \(y_2 = \cos (\theta + \text{30}\text{°})\), \(p < 0\) therefore the graph shifts to the left by \(\text{30}\text{°}\).
Complete a table of values
| θ | \(-\text{360}\)\(\text{°}\) | \(-\text{270}\)\(\text{°}\) | \(-\text{180}\)\(\text{°}\) | \(-\text{90}\)\(\text{°}\) | \(\text{0}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{270}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) |
| \(\cos \theta\) | \(\text{1}\) | \(\text{0}\) | \(-\text{1}\) | \(\text{0}\) | \(\text{1}\) | \(\text{0}\) | \(-\text{1}\) | \(\text{0}\) | \(\text{1}\) |
| \(\cos(\theta + \text{30}\text{°})\) | \(\text{0,87}\) | \(-\text{0,5}\) | \(-\text{0,87}\) | \(\text{0,5}\) | \(\text{0,87}\) | \(-\text{0,5}\) | \(-\text{0,87}\) | \(\text{0,5}\) | \(\text{0,87}\) |
Sketch the cosine graphs
Complete the table
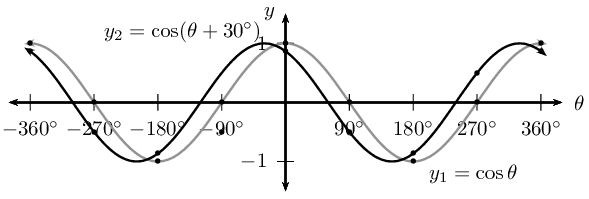
| \(y_1\) | \(y_2\) | |
| period | \(\text{360}\text{°}\) | \(\text{360}\text{°}\) |
| amplitude | \(\text{1}\) | \(\text{1}\) |
| domain | \([-\text{360}\text{°};\text{360}\text{°}]\) | \([-\text{360}\text{°};\text{360}\text{°}]\) |
| range | \([-1;1]\) | \([-1;1]\) |
| maximum turning points | \((-\text{360}\text{°};1)\), \((\text{0}\text{°};1)\) and \((\text{360}\text{°};1)\) | \((-\text{30}\text{°};1)\) and \((\text{330}\text{°};1)\) |
| minimum turning points | \((-\text{180}\text{°};-1)\) and \((\text{180}\text{°};-1)\) | \((-\text{210}\text{°};-1)\) and \((\text{150}\text{°};-1)\) |
| \(y\)-intercept(s) | \((\text{0}\text{°};0)\) | \((\text{0}\text{°};\text{0,87})\) |
| \(x\)-intercept(s) | \((-\text{270}\text{°};0)\), \((-\text{90}\text{°};0)\), \((\text{90}\text{°};0)\) and \((\text{270}\text{°};0)\) | \((-\text{300}\text{°};0)\), \((-\text{120}\text{°};0)\), \((\text{60}\text{°};0)\) and \((\text{240}\text{°};0)\) |
Discovering the characteristics
For functions of the general form: \(f(\theta) = y =\cos (\theta + p)\):
Domain and range
The domain is \(\{ \theta: \theta \in \mathbb{R} \}\) because there is no value for \(\theta\) for which \(f(\theta)\) is undefined.
The range is \(\{ f(\theta): -1 \leq f(\theta) \leq 1, f(\theta) \in \mathbb{R} \}\).
Intercepts
The \(x\)-intercepts are determined by letting \(f(\theta) = 0\) and solving for \(\theta\).
The \(y\)-intercept is calculated by letting \(\theta = \text{0}\text{°}\) and solving for \(f(\theta)\). \begin{align*} y &= \cos (\theta + p) \\ &= \cos (\text{0}\text{°} + p) \\ &= \cos p \end{align*} This gives the point \((\text{0}\text{°};\cos p)\).
Cosine functions of the form \(y = \cos (\theta + p)\)
Textbook Exercise 5.26
Sketch the following functions for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\).
For each function, determine the following:
- Period
- Amplitude
- Domain and range
- \(x\)- and \(y\)-intercepts
- Maximum and minimum turning points
\(f(\theta) =\cos (\theta + \text{45}\text{°})\)
\(g(\theta) =\cos (\theta - \text{30}\text{°})\)
\(h(\theta) =\cos (\theta + \text{60}\text{°})\)
Sketching cosine graphs (EMBH7)
Worked example 24: Sketching a cosine graph
Sketch the graph of \(f(\theta) = \cos (\text{180}\text{°} - 3\theta)\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\).
Examine the form of the equation
Write the equation in the form \(y = \cos k(\theta + p)\). \begin{align*} f(\theta) &= \cos (\text{180}\text{°
To draw a graph of the above function, the standard cosine graph, \(y = \cos \theta\), must be changed in the following ways:
- decrease the period by a factor of \(\text{3}\)
- shift to the right by \(\text{60}\text{°}\).
Complete a table of values
| θ | \(\text{0}\)\(\text{°}\) | \(\text{45}\)\(\text{°}\) | \(\text{90}\)\(\text{°}\) | \(\text{135}\)\(\text{°}\) | \(\text{180}\)\(\text{°}\) | \(\text{225}\)\(\text{°}\) | \(\text{270}\)\(\text{°}\) | \(\text{315}\)\(\text{°}\) | \(\text{360}\)\(\text{°}\) |
| \(f(\theta)\) | \(-\text{1}\) | \(\text{0,71}\) | \(\text{0}\) | \(-\text{0,71}\) | \(\text{1}\) | \(-\text{0,71}\) | \(\text{0}\) | \(\text{0,71}\) | \(-\text{1}\) |
Plot the points and join with a smooth curve
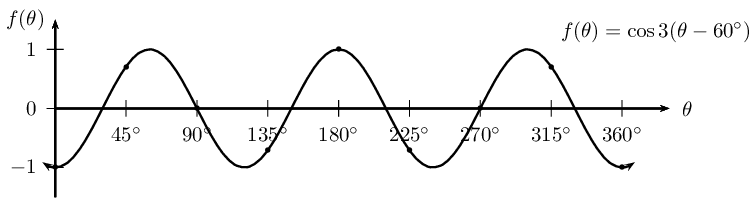
Period: \(\text{120}\)\(\text{°}\)
Amplitude: \(\text{1}\)
Domain: \([\text{0}\text{°};\text{360}\text{°}]\)
Range: \([-1;1]\)
Maximum turning point: \((\text{60}\text{°};1)\), \((\text{180}\text{°};1)\) and \((\text{300}\text{°};1)\)
Minimum turning point: \((\text{0}\text{°}; -1)\), \((\text{120}\text{°};-1)\), \((\text{240}\text{°};-1)\) and \((\text{360}\text{°};-1)\)
\(y\)-intercepts: \((\text{0}\text{°};-1)\)
\(x\)-intercept: \((\text{30}\text{°};0)\), \((\text{90}\text{°};0)\), \((\text{150}\text{°};0)\), \((\text{210}\text{°};0)\), \((\text{270}\text{°};0)\) and \((\text{330}\text{°};0)\)
Worked example 25: Finding the equation of a cosine graph
Given the graph of \(y = a \cos (k\theta + p)\), determine the values of \(a\), \(k\), \(p\) and the minimum turning point.
Determine the value of \(k\)
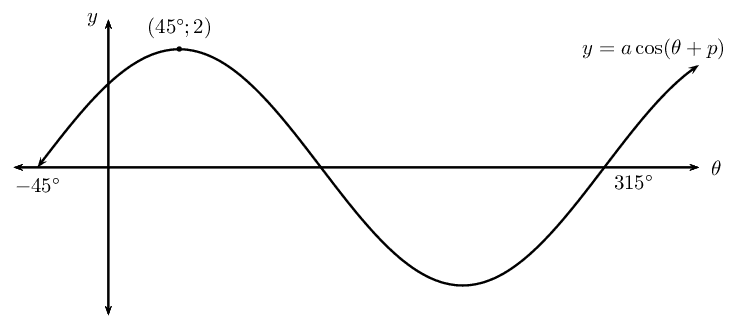
From the sketch we see that the period of the graph is \(\text{360}\text{°}\), therefore \(k = 1\).
\[y = a \cos ( \theta + p)\]
Determine the value of \(a\)
From the sketch we see that the maximum turning point is \((\text{45}\text{°};2)\), so we know that the amplitude of the graph is \(\text{2}\) and therefore \(a = 2\).
\[y = 2 \cos ( \theta + p)\]
Determine the value of \(p\)
Compare the given graph with the standard cosine function \(y = \cos \theta\) and notice the difference in the maximum turning points. We see that the given function has been shifted to the right by \(\text{45}\)\(\text{°}\), therefore \(p = \text{45}\text{°}\).
\[y = 2 \cos ( \theta - \text{45}\text{°})\]
Determine the minimum turning point
At the minimum turning point, \(y = -2\):
\begin{align*} y &= 2 \cos ( \theta - \text{45}\text{°}) \\ -2 &= 2 \cos ( \theta - \text{45}\text{°}) \\ -1 &= \cos ( \theta - \text{45}\text{°}) \\ \cos^{-1}(-1) &= \theta - \text{45}\text{°} \\ \text{180}\text{°} &= \theta - \text{45}\text{°} \\ \text{225}\text{°} &= \theta \end{align*}
This gives the point \((\text{225}\text{°};-2)\).
The cosine function
Textbook Exercise 5.27
Sketch the following graphs on separate axes:
\(y = \cos (\theta + \text{15}\text{°})\) for \(-\text{180}\text{°} \leq \theta \leq \text{180}\text{°}\)
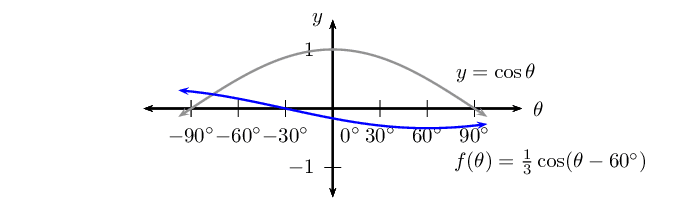
\(f(\theta) = \frac{1}{3} \cos (\theta - \text{60}\text{°})\) for \(-\text{90}\text{°} \leq \theta \leq \text{90}\text{°}\)
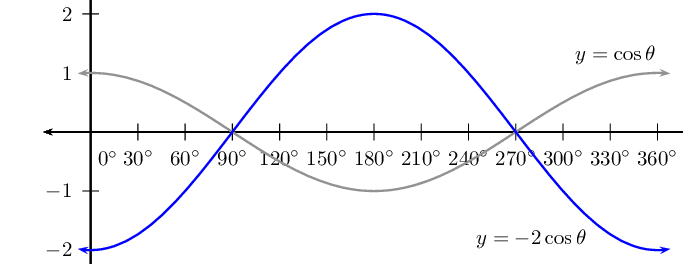
\(y = -2 \cos \theta\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
\(y = \cos (\text{30}\text{°} - \theta)\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\)
\begin{align*}
y &= \cos (\text{30}\text{°} - \theta) \\
&= \cos \left( -(\theta - \text{30}\text{°}) \right) \\
&= \cos \left(\theta - \text{30}\text{°} \right)
\end{align*}
\(g(\theta) = 1 + \cos (\theta - \text{90}\text{°})\) for \(\text{0}\text{°} \leq \theta \leq \text{360}\text{°}\)
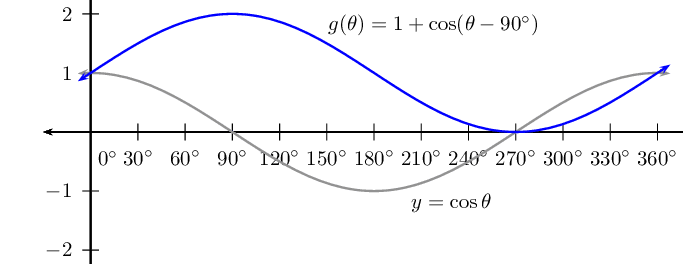
\(y = \cos (2 \theta + \text{60}\text{°})\) for \(-\text{360}\text{°} \leq \theta \leq \text{360}\text{°}\)
Two girls are given the following graph:
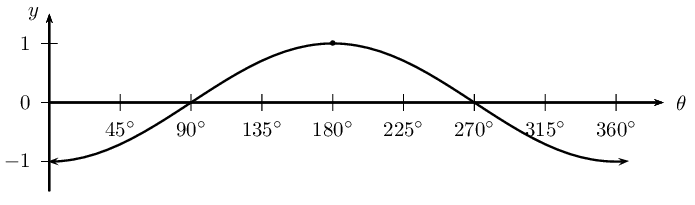
Audrey decides that the equation for the graph is a cosine function of the form \(y = a \cos \theta\). Determine the value of \(a\).
\(a = -1\)
Megan thinks that the equation for the graph is a cosine function of the form \(y = \cos (\theta + p)\). Determine the value of \(p\).
\(p = -\text{180}\text{°}\)
What can they conclude?
\(\cos (\theta - \text{180}\text{°}) = -\cos
\theta\)
|
Previous
5.5 The sine function
|
Table of Contents |
Next
5.7 The tangent function
|