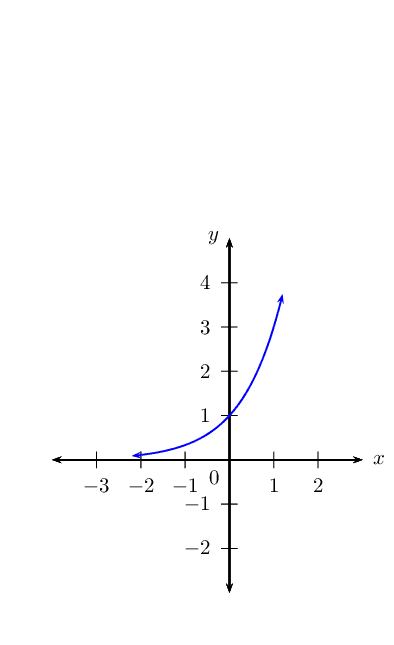
\(y_1 = 3^x\)
5.4 Exponential functions
|
Previous
5.3 Hyperbolic functions
|
Next
5.5 The sine function
|
5.4 Exponential functions (EMBGS)
Revision (EMBGT)
Functions of the form \(y=a{b}^{x}+q\)
Functions of the general form \(y=a{b}^{x}+q\), for \(b>0\), are called exponential functions, where \(a\), \(b\) and \(q\) are constants.
The effects of \(a\), \(b\) and \(q\) on \(f(x) = ab^x + q\):
-
The effect of \(q\) on vertical shift
-
For \(q>0\), \(f(x)\) is shifted vertically upwards by \(q\) units.
-
For \(q<0\), \(f(x)\) is shifted vertically downwards by \(q\) units.
-
The horizontal asymptote is the line \(y = q\).
-
-
The effect of \(a\) on shape
-
For \(a>0\), \(f(x)\) is increasing.
-
For \(a<0\), \(f(x)\) is decreasing. The graph is reflected about the horizontal asymptote.
-
-
The effect of \(b\) on direction
Assuming \(a > 0\):
- If \(b > 1\), \(f(x)\) is an increasing function.
- If \(0 < b < 1\), \(f(x)\) is a decreasing function.
- If \(b \leq 0\), \(f(x)\) is not defined.
|
\(b>1\) |
\(a<0\) |
\(a>0\) |
|
\(q>0\) |
 |
 |
|
\(q<0\) |
 |
 |
|
\(0<b<1\) |
\(a<0\) |
\(a>0\) |
|
\(q>0\) |
 |
 |
|
\(q<0\) |
 |
 |
Revision
Textbook Exercise
5.15
On separate axes, accurately draw each of the following functions:
- Use tables of values if necessary.
- Use graph paper if available.
\(y_2 = -2 \times 3^x\)
\(y_3 = 2 \times 3^x + 1\)
\(y_4 = 3^x - 2\)
Use your sketches of the functions given above to complete the following table (the first column has been completed as an example):
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| value of \(q\) | \(q = 0\) | |||
| effect of \(q\) | no vertical shift | |||
| value of \(a\) | \(a = 1\) | |||
| effect of \(a\) | increasing | |||
| asymptote |
\(x\)-axis, \(y = 0\) |
|||
| domain | \(\{x: x \in \mathbb{R} \}\) | |||
| range | \(\{y: y \in \mathbb{R}, y > 0 \}\) |
| \(y_1\) | \(y_2\) | \(y_3\) | \(y_4\) | |
| value of \(q\) | \(q = 0\) | \(q = 0\) | \(q = 1\) | \(q = 2\) |
| effect of \(q\) | no vertical shift | no vertical shift | shift \(1\) unit up | shift \(2\) units down |
| value of \(a\) | \(a = 1\) | \(a = -2\) | \(a = 2\) | \(a = 1\) |
| effect of \(a\) | increasing | decreasing | increasing | increasing |
| asymptote |
\(x\)-axis, \(y = 0\) |
\(x\)-axis, \(y = 0\) |
\(y = 1\) |
\(y = -2\) |
| domain | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) | \(\{x: x \in \mathbb{R} \}\) |
| range | \(\{y: y \in \mathbb{R}, y > 0 \}\) | \(\{y: y \in \mathbb{R}, y < 0 \}\) | \(\{y: y \in \mathbb{R}, y > 1 \}\) | \(\{y: y \in \mathbb{R}, y > -2 \}\) |
Functions of the form \(y=a{b}^{\left(x+p\right)}+q\) (EMBGV)
We now consider exponential functions of the form \(y=a{b}^{\left(x+p\right)}+q\) and the effects of parameter \(p\).
The effects of \(a\), \(p\) and \(q\) on an exponential graph
-
On the same system of axes, plot the following graphs:
- \(y_1 = 2^x\)
- \(y_2 = 2^{(x - 2)}\)
- \(y_3 = 2^{(x - 1)}\)
- \(y_4 = 2^{(x + 1)}\)
- \(y_5 = 2^{(x + 2)}\)
Use your sketches of the functions above to complete the following table:
\(y_1\) \(y_2\) \(y_3\) \(y_4\) \(y_5\) intercept(s) asymptote domain range effect of \(p\) -
On the same system of axes, plot the following graphs:
- \(y_1 = 2^{(x - 1)} + 2\)
- \(y_2 = 3 \times 2^{(x - 1)} + 2\)
- \(y_3 = \frac{1}{2} \times 2^{(x - 1)} + 2\)
- \(y_4 = 0 \times 2^{(x - 1)} + 2\)
- \(y_5 = -3 \times 2^{(x - 1)} + 2\)
Use your sketches of the functions above to complete the following table:
\(y_1\) \(y_2\) \(y_3\) \(y_4\) \(y_5\) intercept(s) asymptotes domain range effect of \(a\)
The effect of the parameters on \(y = ab^{x + p} + q\)
The effect of \(p\) is a horizontal shift because all points are moved the same distance in the same direction (the entire graph slides to the left or to the right).
-
For \(p>0\), the graph is shifted to the left by \(p\) units.
-
For \(p<0\), the graph is shifted to the right by \(p\) units.
The effect of \(q\) is a vertical shift. The value of \(q\) also affects the horizontal asymptotes, the line \(y = q\).
The value of \(a\) affects the shape of the graph and its position relative to the horizontal asymptote.
-
For \(a>0\), the graph lies above the horizontal asymptote, \(y = q\).
-
For \(a<0\), the graph lies below the horizontal asymptote, \(y = q\).
| \(p>0\) | \(p<0\) | |||
| \(a<0\) | \(a>0\) | \(a<0\) | \(a>0\) | |
| \(q>0\) |  |
 |
 |
 |
|
\(q<0\) |
 |
 |
 |
 |
Discovering the characteristics
For functions of the general form: \(f(x) = y = ab^{(x+p)} + q\):
Domain and range
The domain is \(\left\{x:x\in ℝ\right\}\) because there is no value of \(x\) for which \(f(x)\) is undefined.
The range of \(f(x)\) depends on whether the value for \(a\) is positive or negative.
If \(a>0\) we have: \begin{align*} {b}^{\left(x+p\right)} & > 0 \\ a {b}^{\left(x+p\right)} & > 0 \\ a {b}^{\left(x+p\right)} + q & > q \\ f(x) & > q \end{align*} The range is therefore \(\{ y: y > q, y \in \mathbb{R} \}\).
Similarly, if \(a < 0\), the range is \(\{ y: y < q, y \in \mathbb{R} \}\).
Worked example 14: Domain and range
State the domain and range for \(g(x) = 5 \times 3^{(x+1)} - 1\).
Determine the domain
The domain is \(\{x: x \in \mathbb{R} \}\) because there is no value of \(x\) for which \(g(x)\) is undefined.
Determine the range
The range of \(g(x)\) can be calculated from: \begin{align*} 3^{(x+1)} & > 0\\ 5 \times 3^{(x+1)} & > 0\\ 5 \times 3^{(x+1)} - 1 & > -1\\ \therefore g(x) & > -1 \end{align*} Therefore the range is \(\{g(x): g(x) > -1 \}\) or in interval notation \((-1; \infty)\).
Domain and range
Textbook Exercise
5.16
Give the domain and range for each of the following functions:
\(y = \left( \frac{3}{2} \right)^{(x + 3)}\)
\begin{align*}
\text{Domain: } & \left \{ x: x \in \mathbb{R}
\right \} \\
\text{Range: } & \left \{ y: y > 0, y\in
\mathbb{R} \right \}
\end{align*}
\(f(x) = -5^{(x - 2)} + 1\)
\begin{align*}
\text{Domain: } & \left \{ x: x \in \mathbb{R}
\right \} \\
\text{Range: } & \left \{ y: y < 1, y\in
\mathbb{R} \right \}
\end{align*}
\(y + 3 = 2^{(x + 1)}\)
\begin{align*}
y + 3 &= 2^{(x + 1)} \\
y &= 2^{(x + 1)} - 3 \\
\text{Domain: } & \left \{ x: x \in \mathbb{R}
\right \} \\
\text{Range: } & \left \{ y: y > -3, y\in
\mathbb{R} \right \}
\end{align*}
\(y = n + 3^{(x - m)}\)
\begin{align*}
y &= n + 3^{(x - m)} \\
y &= 3^{(x - m)} + n \\
\text{Domain: } & \left \{ x: x \in \mathbb{R}
\right \} \\
\text{Range: } & \left \{ y: y > n, y\in
\mathbb{R} \right \}
\end{align*}
\(\frac{y}{2} = 3^{(x - 1)} - 1\)
\begin{align*}
\frac{y}{2} &= 3^{(x - 1)} - 1 \\
y &= 2 \times 3^{(x - 1)} - 2 \\
\text{Domain: } & \left \{ x: x \in \mathbb{R}
\right \} \\
\text{Range: } & \left \{ y: y > 2, y\in
\mathbb{R} \right \}
\end{align*}
Intercepts
The \(y\)-intercept:
To calculate the \(y\)-intercept we let \(x=0\). For example, the \(y\)-intercept of \(g(x) = 3 \times 2^{(x + 1)} + 2\) is determined by setting \(x=0\): \begin{align*} g(0) &= 3 \times 2^{(0 + 1)} + 2 \\ &= 3 \times 2 + 2\\ &= 8 \end{align*} This gives the point \((0;8)\).
The \(x\)-intercept:
To calculate the \(x\)-intercept we let \(y=0\). For example, the \(x\)-intercept of \(g(x) = 3 \times 2^{(x + 1)} + 2\) is determined by setting \(y=0\): \begin{align*} 0 &= 3 \times 2^{(x + 1)} + 2 \\ -2 &= 3 \times 2^{(x + 1)} \\ -\frac{2}{3} &= 2^{(x + 1)} \end{align*} which has no real solutions. Therefore, the graph of \(g(x)\) lies above the \(x\)-axis and does not have any \(x\)-intercepts.
Intercepts
Textbook Exercise
5.17
Determine the \(x\)- and \(y\)-intercepts for each of the following functions:
\(f(x) = 2^{(x + 1)} - 8\)
\begin{align*}
\text{For } x=0 \quad y &= 2^{(0 + 1)} - 8 \\
&= 2 - 8 \\
&= -6 \\
\therefore & (0;-6) \\
\text{For } y=0 \quad 0 &= 2^{(x + 1)} - 8 \\
2^3 &= 2^{(x + 1)} \\
\therefore 3 &= x + 1 \\
\therefore 2 &= x \\
\therefore & (2;0)
\end{align*}
\(y = 2 \times 3^{(x - 1)} - \text{18}\)
\begin{align*}
\text{For } x=0 \quad y &= 2 \times 3^{(0 - 1)} - 18
\\
&= \frac{2}{3} -18 \\
&= -17\frac{1}{3} \\
\therefore & (0;-17\frac{1}{3}) \\
\text{For } y=0 \quad 0 &= 2 \times 3^{(x - 1)} - 18
\\
18 &= 2 \times 3^{(x - 1)} \\
9 &= 3^{(x - 1)} \\
3^2 &= 3^{(x - 1)} \\
\therefore 2 &= x - 1 \\
\therefore 3 &= x \\
\therefore & (3;0)
\end{align*}
\(y + 5^{(x + 2)} = 5\)
\begin{align*}
y + 5^{(x + 2)} &= 5 \\
y &= -5^{(x + 2)} + 5 \\
\text{For } x=0 \quad y &= -5^{(0 + 2)} + 5 \\
&= -25 + 5 \\
&= -20 \\
\therefore & (0;-20) \\
\text{For } y=0 \quad 0 &= -5^{(x + 2)} + 5 \\
5^{(x + 2)} &= 5\\
\therefore x + 2 &= 1 \\
\therefore x &= -1 \\
\therefore & (-1;0)
\end{align*}
\(y = \frac{1}{2} \left( \frac{3}{2} \right)^{(x + 3)} - \text{0,75}\)
\begin{align*}
y &= \frac{1}{2} \left( \frac{3}{2} \right)^{(x +
3)} - \text{0,75} \\
y &= \frac{1}{2} \left( \frac{3}{2} \right)^{(x +
3)} - \frac{3}{4} \\
\text{For } x=0 \quad y &= \frac{1}{2} \left(
\frac{3}{2} \right)^{(0 + 3)} - \frac{3}{4} \\
&= \frac{1}{2} \left( \frac{3}{2} \right)^{3} -
\frac{3}{4} \\
&= \frac{1}{2} \left( \frac{27}{8} \right)-
\frac{3}{4} \\
&= \frac{27}{16} - \frac{3}{4} \\
&= \frac{15}{16} \\
\therefore & (0;\frac{15}{16}) \\
\text{For } y=0 \quad 0 &= \frac{1}{2} \left(
\frac{3}{2} \right)^{(x + 3)} - \frac{3}{4} \\
\frac{3}{4} &= \frac{1}{2} \left( \frac{3}{2}
\right)^{(x + 3)} \\
\frac{3}{2} &= \left( \frac{3}{2} \right)^{(x + 3)}
\\
\therefore 1 &= x + 3 \\
\therefore -2 &= x \\
\therefore & (-2;0)
\end{align*}
Asymptote
Exponential functions of the form \(y = ab^{(x+p)} + q\) have a horizontal asymptote, the line \(y = q\).
Worked example 15: Asymptote
Determine the asymptote for \(y = 5 \times 3^{(x+1)} - 1\).
Determine the asymptote
The asymptote of \(g(x)\) can be calculated as: \begin{align*} 3^{(x+1)} & \ne 0\\ 5 \times 3^{(x+1)} & \ne 0\\ 5 \times 3^{(x+1)} - 1 & \ne -1\\ \therefore y & \ne -1 \end{align*} Therefore the asymptote is the line \(y = -1\).
Asymptote
Textbook Exercise
5.18
Give the asymptote for each of the following functions:
\(y = -5^{(x + 1)}\)
\begin{align*}
y &= -5^{(x + 1)} \\
\text{Horizontal asymptote: } \quad y &= 0
\end{align*}
\(y = 3^{(x - 2)} + 1\)
\begin{align*}
y &= 3^{(x - 2)} + 1 \\
\text{Horizontal asymptote: } \quad y &= 1
\end{align*}
\(\left( \frac{3y}{2} \right) = 5^{(x + 3)} - 1\)
\begin{align*}
\left( \frac{3y}{2} \right) &= 5^{(x + 3)} - 1 \\
3y &= 2 \times 5^{(x + 3)} - 2 \\
y &= \frac{2}{3} \times 5^{(x + 3)} - \frac{2}{3} \\
\text{Horizontal asymptote: } \quad y &=
-\frac{2}{3}
\end{align*}
\(y = 7^{(x + 1)} - 2\)
\begin{align*}
y &= 7^{(x + 1)} - 2 \\
\text{Horizontal asymptote: } \quad y &= -2
\end{align*}
\(\frac{y}{2} + 1 = 3^{(x + 2)}\)
\begin{align*}
\frac{y}{2} + 1 &= 3^{(x + 2)} \\
\frac{y}{2} &= 3^{(x + 2)} - 1 \\
y &= 2 \times 3^{(x + 2)} - 2 \\
\text{Horizontal asymptote: } \quad y &= -2
\end{align*}
Sketching graphs of the form \(f(x)=a{b}^{\left(x+p\right)}+q\)
In order to sketch graphs of functions of the form, \(f(x)=a{b}^{\left(x+p\right)}+q\), we need to determine five characteristics:
-
shape
-
\(y\)-intercept
-
\(x\)-intercept
-
asymptote
-
domain and range
Worked example 16: Sketching an exponential graph
Sketch the graph of \(2y = \text{10} \times 2^{(x+1)} - 5\).
Mark the intercept(s) and asymptote. State the domain and range of the function.
Examine the equation of the form \(y = ab^{(x + p)} + q\)
We notice that \(a > 0\) and \(b > 1\), therefore the function is increasing.
Determine the \(y\)-intercept
The \(y\)-intercept is obtained by letting \(x = 0\): \begin{align*} 2y &= \text{10} \times 2^{(0+1)} - 5\\ &= \text{10} \times 2 - 5\\ &= \text{15}\\ \therefore y &= 7\frac{1}{2} \end{align*} This gives the point \((0;7\frac{1}{2})\).
Determine the \(x\)-intercept
The \(x\)-intercept is obtained by letting \(y = 0\): \begin{align*} 0 &= \text{10} \times 2^{(x+1)} - 5\\ 5 &= \text{10} \times 2^{(x+1)} \\ \frac{1}{2} &= 2^{(x+1)}\\ 2^{-1} &= 2^{(x+1)}\\ \therefore -1 &= x + 1 \quad \text{(same base)}\\ -2 &= x \end{align*} This gives the point \((-2;0)\).
Determine the asymptote
The horizontal asymptote is the line \(y = -\frac{5}{2}\).
Plot the points and sketch the graph
State the domain and range
Domain: \(\{ x: x \in \mathbb{R} \}\)
Range: \(\{ y: y > -\frac{5}{2}, y \in \mathbb{R} \}\)
Finding the equation of an exponential function from the graph
Worked example 17: Finding the equation of an exponential function from the graph
Use the given graph of \(y = -2 \times 3^{(x + p)} + q\) to determine the values of \(p\) and \(q\).
Examine the equation of the form \(y = ab^{(x + p)} + q\)
From the graph we see that the function is decreasing. We also note that \(a = -2\) and \(b = 3\).
We need to solve for \(p\) and \(q\).
Use the asymptote to determine \(q\)
The horizontal asymptote \(y = 6\) is given, therefore we know that \(q = 6\). \[y = -2 \times 3^{(x + p)} + 6\]
Use the \(x\)-intercept to determine \(p\)
Substitute \((2;0)\) into the equation and solve for \(p\): \begin{align*} y &= -2 \times 3^{(x + p)} + 6 \\ 0 &= -2 \times 3^{(2 + p)} + 6 \\ -6 &= -2 \times 3^{(2 + p)} \\ 3 &= 3^{(2 + p)} \\ \therefore 1 &= 2 + p \quad \text{(same base)}\\ \therefore p &= -1 \end{align*}
Write the final answer
\[y = -2 \times 3^{(x - 1)} + 6\]
Mixed exercises
Textbook Exercise
5.19
Given the graph of the hyperbola of the form \(h(x) = \frac{k}{x}\), \(x < 0\), which passes though the point \(A(-\frac{1}{2}; -6)\).
Show that \(k=3\).
\begin{align*}
y &=\frac{k}{x} \\
\text{Subst. } (-\frac{1}{2}; -6) \qquad -6
&=\frac{k}{-\frac{1}{2}} \\
-6 \times -\frac{1}{2} &= k \\
\therefore k &=3 \\
\therefore h(x) &= \frac{3}{x}
\end{align*}
Write down the equation for the new function formed if \(h(x)\):
is shifted \(\text{3}\) units vertically upwards
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore y &\Rightarrow y - 3 \\
y - 3 &=\frac{3}{x} \\
y &=\frac{3}{x}+3
\end{align*}
is shifted to the right by \(\text{3}\) units
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore x &\Rightarrow x - 3 \\
y &=\frac{3}{x -3}
\end{align*}
is reflected about the \(y\)-axis
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore x &\Rightarrow -x \\
y &=\frac{3}{x -3}
\end{align*}
is shifted so that the asymptotes are \(x = 0\) and \(y = -\frac{1}{4}\)
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore p=0 &\text{ and } q =
-\frac{1}{4} \\
y &=\frac{3}{x} -\frac{1}{4}
\end{align*}
is shifted upwards to pass through the point \((-1;1)\)
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore y &\Rightarrow y + m \\
y &=\frac{3}{x} + m \\
\text{Subst.} (-1;1) \qquad 1 &=
\frac{3}{-1} + m \\
1 + 3 &= + m \\
\therefore m &= 4 \\
\therefore y &=\frac{3}{x} + 4
\end{align*}
is shifted to the left by \(\text{2}\) units and \(\text{1}\) unit vertically downwards (for \(x < 0\))
\begin{align*}
h(x) &= \frac{3}{x} \\
\therefore x &\Rightarrow x + 2 \\
\therefore y &\Rightarrow y + 1 \\
y + 1 &=\frac{3}{x + 2} \\
\therefore y &=\frac{3}{x + 2} - 1
\end{align*}
Given the graphs of \(f(x) = a(x+p)^2\) and \(g(x) = \frac{a}{x}\).
The axis of symmetry for \(f(x)\) is \(x = -1\) and \(f(x)\) and \(g(x)\) intersect at point \(M\). The line \(y = 2\) also passes through \(M\).
Determine:
the coordinates of \(M\)
\(f(x)\) is symmetrical about the line \(x = -1\), therefore \(M(-2;2)\).
the equation of \(g(x)\)
\begin{align*}
g(x) &= \frac{a}{x} \\
\text{Subst. } M(-2;2) \qquad 2 &=
\frac{a}{-2} \\
\therefore a &= -4 \\
\therefore g(x)&=\frac{-4}{x}
\end{align*}
the equation of \(f(x)\)
\begin{align*}
f(x) &= a(x + p)^2 + q \\
\text{No vertical shift } \therefore q &= 0
\\
\text{Axis of symmetry } x = -1 \qquad
\therefore f(x) &= a(x + 1)^2 \\
\text{Subst. } M(-2;2) \qquad 2 &= a(-2 +
1)^2 \\
2 &= a(-1)^2 \\
\therefore a &= 2 \\
\therefore f(x) &= 2(x + 1)^2
\end{align*}
the values for which \(f(x) < g(x)\)
\(- 2 < x < 0\)
the range of \(f(x)\)
\(\text{Range: }\left \{ y: y\in
\mathbb{R}, y \geq 0 \right \}\)
On the same system of axes, sketch:
the graphs of \(k(x) = 2(x + \frac{1}{2})^2 - 4\frac{1}{2}\) and \(h(x) = 2^{(x + \frac{1}{2})}\). Determine all intercepts, turning point(s) and asymptotes.
the reflection of \(h(x)\) about the \(x\)-axis. Label this function as \(j(x)\).
Sketch the graph of \(y = ax^2 + bx + c\) for:
\(a < 0\), \(b > 0\), \(b^2 < 4ac\)
\(a > 0\), \(b > 0\), one root \(=0\)
On separate systems of axes, sketch the graphs:
\(y = \frac{2}{x - 2}\)
\(y = \frac{2}{x} - 2\)
\(y = -2^{(x - 2)}\)
For the diagrams shown below, determine:
- the equations of the functions; \(f(x) = a(x + p)^2 + q\), \(g(x)=ax^2 + q\), \(h(x) = \frac{a}{x}, x < 0\) and \(k(x)=b^x + q\)
- the axes of symmetry of each function
- the domain and range of each function
\begin{align*}
f(x) &= a(x + p)^2 + q \\
\text{From turning point: } p= -2 &\text{
and } q = 3 \\
\therefore f(x) &= a(x - 2 )^2 + 3 \\
\text{Subst. } (0;0) \qquad 0 &= a(0 - 2)^2
+ 3 \\
-3 &= 4a \\
\therefore a &= -\frac{3}{4} \\
f(x) &= -\frac{3}{4}(x - 2)^2 + 3 \\
\text{Axes of symmetry: } x &= 2 \\
\text{Domain: } & \left \{ x:x \in
\mathbb{R} \right \} \\
\text{Range: } & \left \{ y:y \in
\mathbb{R}, y \leq 3 \right \}
\end{align*}
\begin{align*}
g(x) &= ax^2 + q \\
\text{From turning point: } p= 0 &\text{ and
} q = -2 \\
\therefore g(x) &= a(x)^2 - 2 \\
\text{Subst. } (-2;-1) \qquad -1 &= a(-2 )^2
- 2\\
-1 &= 4a - 2\\
1 &= 4a - 2\\
\therefore a &= \frac{1}{4} \\
g(x) &= \frac{1}{4}x^2 -2 \\
\text{Axes of symmetry: } x &= 0 \\
\text{Domain: } & \left \{ x:x \in
\mathbb{R} \right \} \\
\text{Range: } & \left \{ y:y \in
\mathbb{R}, y \geq -2 \right \} \\
h(x) &= \frac{a}{x + p} + q \\
\text{From graph: } p= 0 &\text{ and } q = 0
\\
h(x) &= \frac{a}{x} \\
\text{Subst. } (-2;-1) \qquad -1
&=\frac{a}{-2} \\
2 &= a \\
\therefore h(x) &= \frac{2}{x} \\
\text{Axes of symmetry: } y &= x \\
\text{Domain: } &\left \{ x:x \in
\mathbb{R}, x < 0 \right \} \\
\text{Range: } & \left \{ y:y \in
\mathbb{R}, y < 0 \right \}
\end{align*}
\begin{align*}
y &= 2^{x} + \frac{1}{2} \\
\text{Reflect about } x = 0 \qquad \therefore x
&\\Rightarrow -x \\
\therefore k(x) &= 2^{-x} + \frac{1}{2} \\
&= \left( \frac{1}{2} \right)^{x} +
\frac{1}{2} \\
\text{Domain: } & \left \{ x:x \in
\mathbb{R} \right \} \\
\text{Range: } & \left \{ y:y \in
\mathbb{R}, y > \frac{1}{2} \right \}
\end{align*}
Given the graph of the function \(Q(x) = a^x\).
Show that \(a = \frac{1}{3}\).
\begin{align*}
y&=a^x \\
\text{Subst.} \left( 1;\frac{1}{3} \right)
\qquad \frac{1}{3} &=a^{1} \\
\therefore a &= \frac{1}{3}
\end{align*}
Find the value of \(p\) if the point \((-2;p)\) is on \(Q\).
\begin{align*}
Q(x) &= \left( \frac{1}{3} \right)^x \\
\text{Subst.} \left( -2;p \right) p &=
\left( \frac{1}{3} \right)^{-2} \\
p &= 9
\end{align*}
Calculate the average gradient of the curve between \(x = -2\) and \(x = 1\).
\begin{align*}
\text{Average gradient} &= \frac{\left (
\frac{1}{3} \right )^{-2} - \left ( \frac{1}{3}
\right )^1}{-2-(1)} \\
&= \frac{9-\frac{1}{3}}{-3} \\
&=\frac{8\frac{2}{3}}{-3} \\
&= \frac{-26}{9} \\
&= -2\frac{8}{9}
\end{align*}
Determine the equation of the new function formed if \(Q\) is shifted \(\text{2}\) units vertically downwards and \(\text{2}\) units to the left.
\begin{align*}
Q(x) &= \left( \frac{1}{3} \right)^x \\
\therefore x & \Rightarrow x + 2 \\
\therefore y & \Rightarrow y + 2 \\
y + 2 &= \left( \frac{1}{3} \right)^{x + 2}
\\
y &= \left( \frac{1}{3} \right)^{x + 2} -2
\end{align*}
Find the equation for each of the functions shown below:
\(f(x) = 2^x + q\)
\(g(x) = mx + c\)
\begin{align*}
f(x) &= 2^x + q \\
\text{Subst. } (0; -\frac{1}{2}) \quad
-\frac{1}{2} &= 2^{0} + q \\
-\frac{1}{2} &= 1 + q \\
\therefore q &= -\frac{3}{2} \\
\therefore f(x) &=2^x-\frac{3}{2} \\
g(x) &= mx +c \\
\text{Subst. } (0; -\frac{1}{2}) \quad
-\frac{1}{2} &= m(0) + c \\
\therefore c &= -\frac{1}{2} \\
g(x) &= mx -\frac{1}{2} \\
\text{Subst. } (-2;0) \quad 0 &= m(-2)
-\frac{1}{2} \\
\frac{1}{2} &= -2m \\
\therefore m &= -\frac{1}{4} \\
\therefore g(x) &= -\frac{1}{4}x-\frac{1}{2}
\end{align*}
\(h(x) = \frac{k}{x + p} + q\)
\begin{align*}
h(x) &= \frac{k}{x + p} + q \\
\text{From graph: } \quad p = -2 \\
h(x) &= \frac{k}{x + 2} + q \\
\text{Subst. } (0; -\frac{1}{2}) \quad
-\frac{1}{2} &= \frac{k}{2} + q \\
-1 &= k + 2q \ldots (1)\\
\text{Subst. } (1;0) \quad 0 &= \frac{k}{1 +
2} + q \\
0 &= k + 3q \ldots (2)\\
(2) - (1): \qquad 1 &= 0 + q \\
\therefore q &= 1 \\
\text{and } k &= -3\\
\therefore h(x) &= -\frac{3}{x + 2} + 1
\end{align*}
Given: the graph of \(k(x) = -x^2 + 3x + \text{10}\) with turning point at \(D\). The graph of the straight line \(h(x) = mx + c\) passing through points \(B\) and \(C\) is also shown.
Determine:
the lengths \(AO\), \(OB\), \(OC\) and \(DE\)
\begin{align*}
y &=-x^2+3x+10 \\
\text{Let } y &= 0 \\
0 &=-x^2+3x+10 \\
&= x^2-3x-10\\
&= (x-5)(x+2)\\
\therefore x=5 &\text{ or }x =-2 \\
\therefore AO &= \text{2}\text{ units} \\
\therefore BO &=\text{5}\text{ units} \\
CO&=\text{10}\text{ units}\\
\text{Axes of symmetry: } x &=-\frac{5 -
2}{2} \\
&=\frac{3}{2} \\
\text{Subst. } x &= \frac{3}{2} \\
y &=-\left ( \frac{3}{2} \right
)^2+3\frac{3}{2}+10 \\
&=12\frac{1}{4} \\
\therefore DE &= \text{12,25}\text{ units}
\end{align*}
the equation of \(DE\)
\(DE = 12\frac{1}{4}\)
the equation of \(h(x)\)
\begin{align*}
h(x) & = mx + c \\
h(x) & = mx + 10 \\
\text{Subst. } (5;0) \qquad 0 &= m(5) + 10
\\
-10 &= 5m \\
\therefore m &= -2 \\
\therefore h(x) &=-2x+10
\end{align*}
the \(x\)-values for which \(k(x) < 0\)
\(\left \{ x: x\in \mathbb{R}, x
< -2 \text{ and } x > 5 \right \}\)
the \(x\)-values for which \(k(x) \geq h(x)\)
\(\left \{ x: x\in \mathbb{R}, 0
\leq x \leq 5 \right \}\)
the length of \(DF\)
\begin{align*}
\text{At } x = \frac{3}{2} k(x) &=
12\frac{1}{4} \\
\text{At } x = \frac{3}{2} h(x) &= -2 \left(
\frac{3}{2} \right) + 10 \\
&= -3 + 10 \\
&= 7\\
\therefore DF &= 12\frac{1}{4} - 7 \\
&= 12\frac{1}{4} - 7 \\
&= \text{5,25}\text{ units}
\end{align*}
Trigonometric functions are examined in PAPER 2.
|
Previous
5.3 Hyperbolic functions
|
Table of Contents |
Next
5.5 The sine function
|