5.2 Average gradient

5.2 Average gradient (EMBGN)

We notice that the gradient of a curve changes at every point on the curve, therefore we need to work with the average gradient. The average gradient between any two points on a curve is the gradient of the straight line passing through the two points.

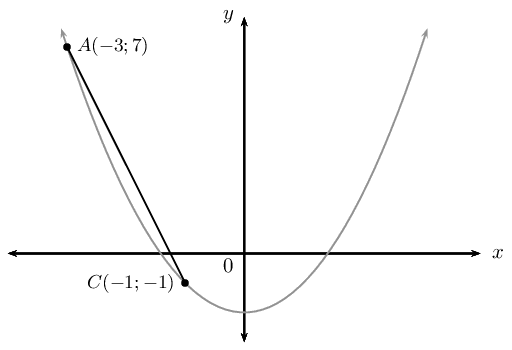
For the diagram above, the gradient of the line $AC$ is

What happens to the gradient if we fix the position of one point and move the second point closer to the fixed point?

Gradient at a single point on a curve

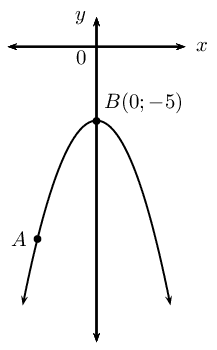
The curve shown here is defined by $y=-2{x}^{2}-5$. Point $B$ is fixed at $\left(0;-5\right)$ and the position of point $A$ varies.

Complete the table below by calculating the $y$-coordinates of point $A$ for the given $x$-coordinates and then calculating the average gradient between points $A$ and $B$.

$x_A$	$y_A$	Average gradient
$-\text{2}$
$-\text{1,5}$
$-\text{1}$
$-\text{0,5}$
$\text{0}$
$\text{0,5}$
$\text{1}$
$\text{1,5}$
$\text{2}$

1. What happens to the average gradient as $A$ moves towards $B$?
2. What happens to the average gradient as $A$ moves away from $B$?
3. What is the average gradient when $A$ overlaps with $B$?

In the example above, the gradient of the straight line that passes through points $A$ and $C$ changes as $A$ moves closer to $C$. At the point where $A$ and $C$ overlap, the straight line only passes through one point on the curve. This line is known as a tangent to the curve.

We therefore introduce the idea of the gradient at a single point on a curve. The gradient at a point on a curve is the gradient of the tangent to the curve at the given point.

Worked example 7: Average gradient

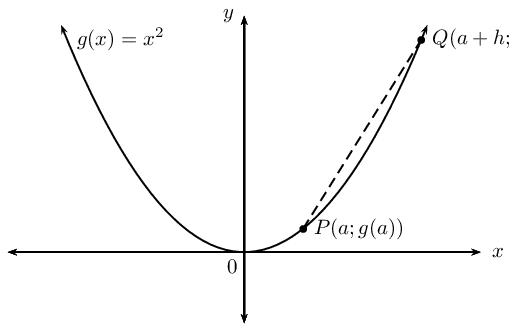
1. Find the average gradient between two points $P\left(a;g(a)\right)$ and $Q\left(a+h;g(a+h)\right)$ on a curve $g(x)={x}^{2}$.
2. Determine the average gradient between $P\left(2;g(2)\right)$ and $Q\left(5;g(5)\right)$.
3. Explain what happens to the average gradient if $Q$ moves closer to $P$.

Assign labels to the $x$-values for the given points

$$\begin{align*} x_1 &= a \\ x_2 &= a + h \end{align*}$$

Determine the corresponding $y$-coordinates

Using the function $g(x) = x^2$, we can determine:

$$y_1 = g(a) = a^2$$ $$\begin{align*} y_2 &= g(a + h) \\ &= (a + h)^2 \\ &= a^2 + 2ah + h^2 \end{align*}$$

Calculate the average gradient

$$\begin{align*} \frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}} &= \frac{\left({a}^{2}+2ah+{h}^{2}\right)-\left({a}^{2}\right)}{\left(a+h\right)-\left(a\right)} \\ &= \frac{{a}^{2}+2ah+{h}^{2}-{a}^{2}}{a+h-a} \\ &= \frac{2ah+{h}^{2}}{h} \\ &= \frac{h(2a+h)}{h} \\ &= 2a+h \end{align*}$$ The average gradient between $P\left(a;g(a)\right)$ and $Q\left(a+h;g(a+h)\right)$ on the curve $g(x)={x}^{2}$ is $2a+h$.

Calculate the average gradient between $P\left(2;g(2)\right)$ and $Q\left(5;g(5)\right)$

The $x$-coordinate of $P$ is $a$ and the $x$-coordinate of $Q$ is $a+h$ therefore if we know that $a=2$ and $a+h=5$, then $h=3$.

The average gradient is therefore

$2a+h=2\left(2\right)+\left(3\right)=7$

When $Q$ moves closer to $P$

When point $Q$ moves closer to point $P$, $h$ gets smaller.

When the point $Q$ overlaps with the point $P$, $h=0$ and the gradient is given by $2a$.

We can write the equation for average gradient in another form. Given a curve $f(x)$ with two points $P$ and $Q$ with $P\left(a;f(a)\right)$ and $Q\left(a+h;f(a+h)\right)$. The average gradient between $P$ and $Q$ is:

Worked example 8: Average gradient

Given $f(x) = -2x^2$.

1. Draw a sketch of the function and determine the average gradient between the points $A$, where $x = 1$, and $B$, where $x = 3$.

2. Determine the gradient of the curve at point $A$.

Examine the form of the equation

From the equation we see that $a < 0$, therefore the graph is a “frown” and has a maximum turning point. We also see that when $x = 0$, $y = 0$, therefore the graph passes through the origin.

Draw a rough sketch

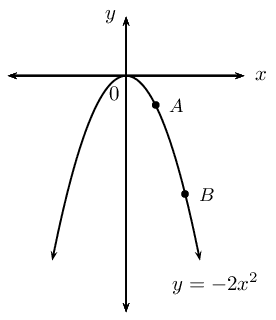
Calculate the average gradient between $A$ and $B$

$$\begin{align*} \text{Average gradient} &= \frac{f(3) - f(1)}{3 - 1} \\ &= \frac{-2(3)^2 - (-2(1)^2)}{2} \\ &= \frac{-18 + 2}{2} \\ &= \frac{-16}{2} \\ &= -8 \end{align*}$$

Calculate the average gradient for $f(x)$

$$\begin{align*} \text{Average gradient} &= \frac{f(a + h) - f(a)}{(a + h) - a} \\ &= \frac{-2(a + h)^2 - (-2a^2)}{h} \\ &= \frac{-2a^2 - 4ah - 2h^2 + 2a^2}{h} \\ &= \frac{-4ah - 2h^2}{h} \\ &= \frac{h(-4a - 2h)}{h} \\ &= -4a - 2h \end{align*}$$ At point $A$, $h = 0$ and $a = 1$.

Therefore

$$\begin{align*} \text{Average gradient} &= -4a - 2h \\ &= -4(1) - 2(0) \\ &= -4 \end{align*}$$

Interactive Exercise 5.7

Textbook Exercise 5.8

Determine the average gradient of the curve \(f(x)=x\left(x+3\right)\) between \(x=5\) and \(x=3\).

\(\text{11}\)

Hence, state what you can deduce about the function \(f\) between \(x=5\) and \(x=3\).

Solution not available at present

\(A\left(1;3\right)\) is a point on \(f(x)=3{x}^{2}\).

Draw a sketch of \(f(x)\) and label point \(A\).

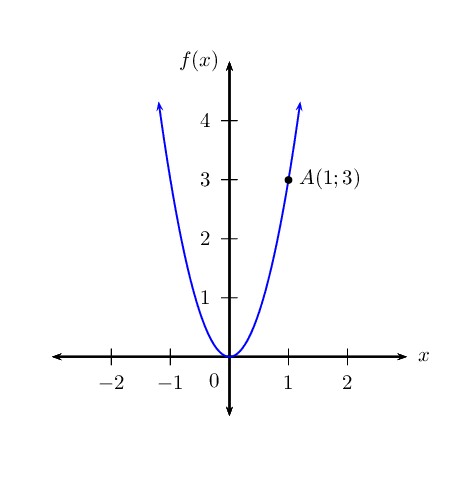
Determine the gradient of the curve at point \(A\).

\(\text{6}\)

Determine the equation of the tangent line at \(A\).

\(y = 6x - 3\)

Given: \(g(x) = -x^2 + 1\).

Draw a sketch of \(g(x)\).

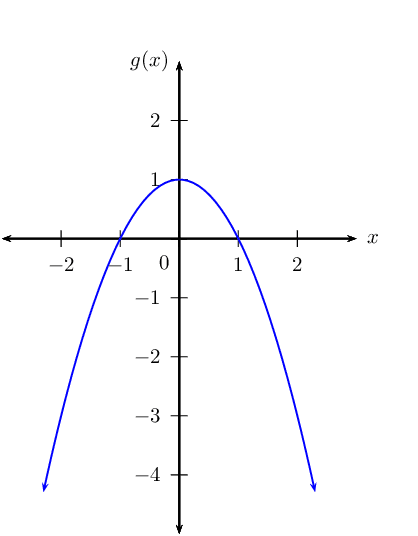
Determine the average gradient of the curve between \(x=-2\) and \(x=1\).

\(\text{1}\)

Determine the gradient of \(g\) at \(x=2\).

\(\text{4}\)

Determine the gradient of \(g\) at \(x=0\).

\(\text{0}\)

Try the textbook questions