End of chapter exercises
|
Previous
8.3 Summary
|
Next
9.1 Revision
|
End of chapter exercises
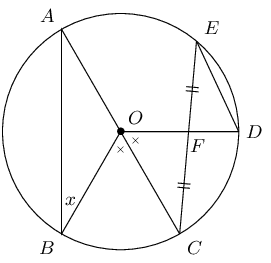
\(AOC\) is a diameter of the circle with centre \(O\). \(F\) is the mid-point of chord \(EC\). \(B\hat{O}C = C\hat{O}D\) and \(\hat{B} = x\). Express the following angles in terms of \(x\), stating reasons:
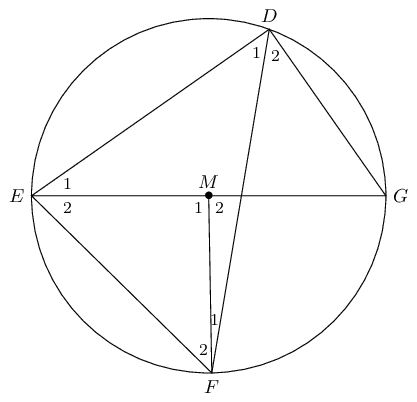
\(D\), \(E\), \(F\) and \(G\) are points on circle with centre \(M\). \(\hat{F}_1 = \text{7}\text{°}\) and \(\hat{D}_2 = \text{51}\text{°}\). Determine the sizes of the following angles, stating reasons:
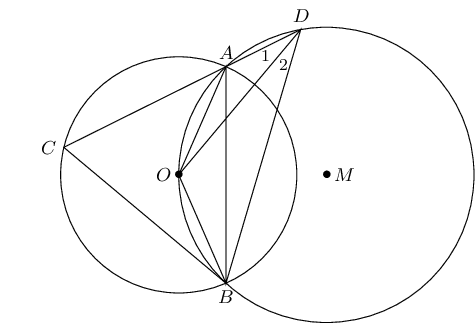
\(O\) is a point on the circle with centre \(M\). \(O\) is also the centre of a second circle. \(DA\) cuts the smaller circle at \(C\) and \(\hat{D}_1 = x\). Express the following angles in terms of \(x\), stating reasons:
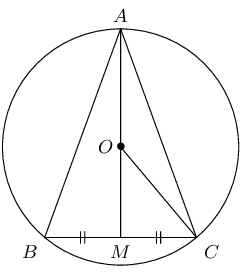
\(O\) is the centre of the circle with radius \(\text{5}\) \(\text{cm}\) and chord \(BC = \text{8}\text{ cm}\). Calculate the lengths of:

\(AO \parallel CB\) in circle with centre \(O\). \(A\hat{O}B = \text{70}\text{°}\) and \(O\hat{A}C = x\). Calculate the value of \(x\), giving reasons.
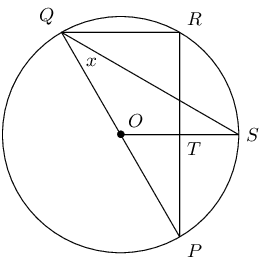
\(PQ\) is a diameter of the circle with centre \(O\). \(SQ\) bisects \(P\hat{Q}R\) and \(P\hat{Q}S = x\).
Write down two other angles that are also equal to \(x\).
Calculate \(P\hat{O}S\) in terms of \(x\), giving reasons.
Prove that \(OS\) is a perpendicular bisector of \(PR\).

\(B\hat{O}D\) is a diameter of the circle with centre \(O\). \(AB = AD\) and \(O\hat{C}D = \text{35}\text{°}\). Calculate the value of the following angles, giving reasons:
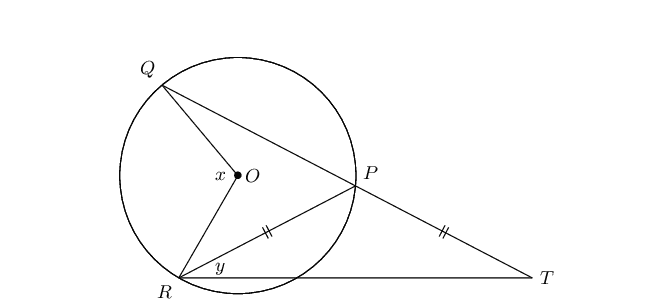
\(QP\) in the circle with centre \(O\) is protracted to \(T\) so that \(PR = PT\). Express \(y\) in terms of \(x\).

\(O\) is the centre of the circle with diameter \(AB\). \(CD \perp AB\) at \(P\) and chord \(DE\) cuts \(AB\) at \(F\). Prove that:
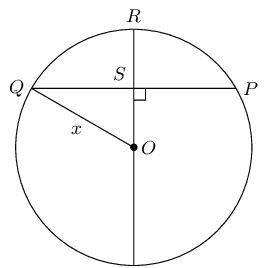
In the circle with centre \(O\), \(OR \perp QP\), \(PQ = \text{30}\text{ mm}\) and \(RS = \text{9}\text{ mm}\). Determine the length of \(OQ\).
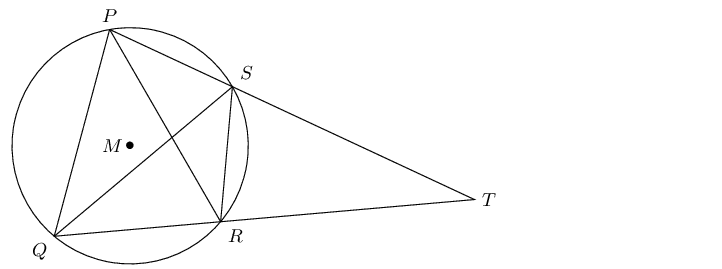
\(P\), \(Q\), \(R\) and \(S\) are points on the circle with centre \(M\). \(PS\) and \(QR\) are extended and meet at \(T\). \(PQ = PR\) and \(P\hat{Q}R = \text{70}\text{°}\).
Determine, stating reasons, three more angles equal to \(\text{70}\text{°}\).
If \(Q\hat{P}S = \text{80}\text{°}\), calculate \(S\hat{R}T\), \(S\hat{T}R\) and \(P\hat{Q}S\).
Explain why \(PQ\) is a tangent to the circle \(QST\) at point \(Q\).
Determine \(P\hat{M}Q\).
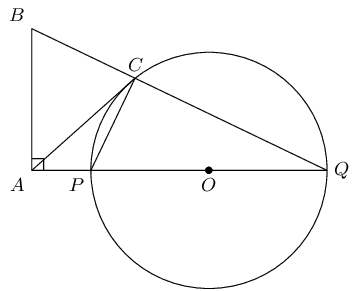
\(POQ\) is a diameter of the circle with centre \(O\). \(QP\) is protruded to \(A\) and \(AC\) is a tangent to the circle. \(BA \perp AQ\) and \(BCQ\) is a straight line. Prove:
\(BAPC\) is a cyclic quadrilateral
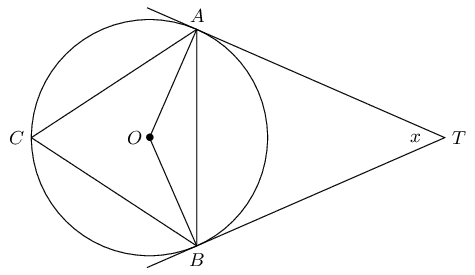
\(TA\) and \(TB\) are tangents to the circle with centre \(O\). \(C\) is a point on the circumference and \(A\hat{T}B = x\). Express the following in terms of \(x\), giving reasons:
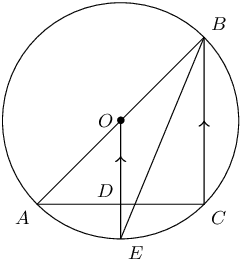
\(AOB\) is a diameter of the circle \(AECB\) with centre \(O\). \(OE \parallel BC\) and cuts \(AC\) at \(D\).
Prove \(AD = DC\)
Show that \(A\hat{B}C\) is bisected by \(EB\)
If \(O\hat{E}B = x\), express \(B\hat{A}C\) in terms of \(x\)
Calculate the radius of the circle if \(AC = \text{10}\text{ cm}\) and \(DE = \text{1}\text{ cm}\)
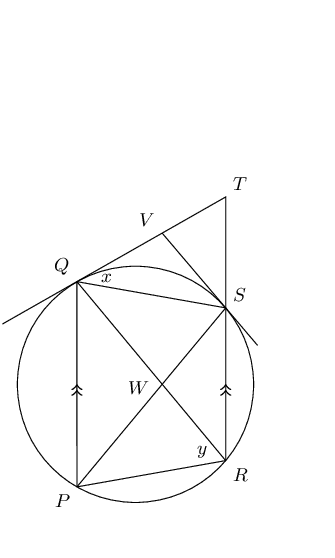
\(PQ\) and \(RS\) are chords of the circle and \(PQ \parallel RS\). The tangent to the circle at \(Q\) meets \(RS\) protruded at \(T\). The tangent at \(S\) meets \(QT\) at \(V\). \(QS\) and \(PR\) are drawn.
Let \(T\hat{Q}S = x\) and \(Q\hat{R}P = y\). Prove that:
\(QVSW\) is a cyclic quadrilateral
\(W\) is the centre of the circle
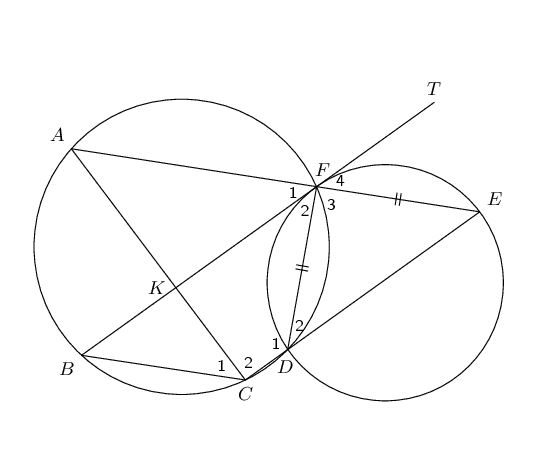
The two circles shown intersect at points \(F\) and \(D\). \(BFT\) is a tangent to the smaller circle at \(F\). Straight line \(AFE\) is drawn such that \(DF = EF\). \(CDE\) is a straight line and chord \(AC\) and \(BF\) cut at \(K\). Prove that:
\(BCEF\) is a parallelogram
|
Previous
8.3 Summary
|
Table of Contents |
Next
9.1 Revision
|
