4.4 Parallel lines | Analytical geometry

4.4 Parallel lines (EMBGF)

Parallel lines

Draw a sketch of the line passing through the points \(P(-1;0)\) and \(Q(1;4)\) and the line passing through the points \(R(1;2)\) and \(S(2;4)\).
Label and measure \(\alpha\) and \(\beta\), the angles of inclination of straight lines \(PQ\) and \(RS\) respectively.
Describe the relationship between \(\alpha\) and \(\beta\).
“\(\alpha\) and \(\beta\) are alternate angles, therefore \(PQ \parallel RS\).” Is this a true statement? If not, provide a correct statement.
Use your calculator to determine \(\tan \alpha\) and \(\tan \beta\).
Complete the sentence: \(\ldots \ldots\) lines have \(\ldots \ldots\) angles of inclination.
Determine the equations of the straight lines \(PQ\) and \(RS\).
What do you notice about \(m_{PQ}\) and \(m_{RS}\)?
Complete the sentence: \(\ldots \ldots\) lines have \(\ldots \ldots\) gradients.

Another method of determining the equation of a straight line is to be given a point on the unknown line, \(\left({x}_{1};{y}_{1}\right)\), and the equation of a line which is parallel to the unknown line.

Let the equation of the unknown line be \(y = m_1x + c_1\) and the equation of the given line be \(y = m_2x + c_2\).

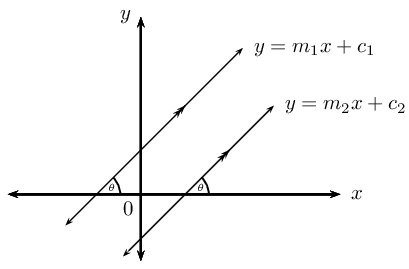
If the two lines are parallel then

\[m_1 = m_2\]

Important: when determining the gradient of a line using the coefficient of \(x\), make sure the given equation is written in the gradient–intercept (standard) form.

\[y=mx+c\]

Substitute the value of \(m_2\) and the given point \(\left({x}_{1};{y}_{1}\right)\), into the gradient–intercept form of a straight line equation

\[y - y_1 = m(x - x_1)\]

and determine the equation of the unknown line.

Worked example 11: Parallel lines

Determine the equation of the line that passes through the point \((-1;1)\) and is parallel to the line \(y - 2x + 1 = 0\).

Write the equation in gradient–intercept form

We write the given equation in gradient–intercept form and determine the value of \(m\).

\[y = 2x - 1\]

We know that the two lines are parallel, therefore \(m_1 = m_2 = 2\).

Write down the gradient–point form of the straight line equation

\[y - y_1 = m(x - x_1)\]

Substitute \(m = 2\)

\[y - y_1 = 2(x - x_1)\]

Substitute the given point \((-1;1)\)

\begin{align*} y - 1 & = 2(x - (-1)) \\ y - 1& = 2x + 2\\ y & = 2x + 2 + 1\\ &= 2x + 3 \end{align*}

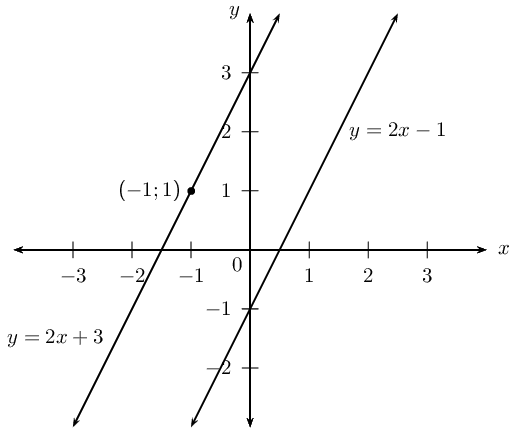
A sketch was not required, but it is always helpful and can be used to check answers.

Write the final answer

The equation of the straight line is \(y = 2x + 3\).

temp text

Worked example 12: Parallel lines

Line \(AB\) passes through the point \(A(0;3)\) and has an angle of inclination of \(\text{153,4}\)\(\text{°}\). Determine the equation of the line \(CD\) which passes through the point \(C(2;-3)\) and is parallel to \(AB\).

Use the given angle of inclination to determine the gradient

\begin{align*} m_{AB} & = \tan \theta \\ & = \tan \text{153,4}\text{°} \\ & = -\text{0,5} \end{align*}

Parallel lines have equal gradients

Since we are given \(AB \parallel CD\),

\[m_{CD} = m_{AB} = -\text{0,5}\]

Write down the gradient–point form of a straight line equation

\[y - y_1 = m(x - x_1)\]

Substitute the gradient \(m_{CD} = -\text{0,5}\).

\[y - y_1 = -\frac{1}{2}(x - x_1)\]

Substitute the given point \((2;-3)\).

\begin{align*} y - (-3) & = -\frac{1}{2}(x - 2) \\ y + 3 & = -\frac{1}{2}x + 1\\ y & = -\frac{1}{2}x - 2 \end{align*}

A sketch was not required, but it is always useful.

Write the final answer

The equation of the straight line is \(y = -\frac{1}{2}x - 2\).

Video: 22N3

Parallel lines

Textbook Exercise 4.7

\(y + 2 x = 1\) and \(-2x + 3 = y\)

\begin{align*} y + 2 x &= 1 \\ y &= -2x + 1 \\ \therefore m_1 &= -2 \\ -2x + 3 &= y \\ \therefore m_2 &= -2 \\ \therefore m_1 &= m_2 \end{align*}

\(\therefore\)Parallel lines.

\(\frac{y}{3} + x + 5 = 0\) and \(2y + 6x = 1\)

\begin{align*} \frac{y}{3} + x + 5 &= 0\\ \frac{y}{3} &= -x - 5 \\ y &= -3x - 15 \\ \therefore m_1 &= -3 \\ 2y + 6x &= 1 \\ 2y &= -6x + 1 \\ y &= -3x + \frac{1}{3} \\ \therefore m_2 &= -3 \\ \therefore m_1 &= m_2 \end{align*}

\(\therefore\)Parallel lines.

\(y = 2x - 7\) and the line passing through \((1;-2)\) and \((\frac{1}{2};-1)\)

\begin{align*} y &= 2x - 7 \\ \therefore m_1 &= 2 \\ m_2 &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{-1 + 2}{\frac{1}{2} - 1} \\ &= \frac{1}{\frac{1}{2}} \\ \therefore m_2 &= 2 \\ \therefore m_1 &= m_2 \end{align*}

\(\therefore\)Parallel lines.

\(y + 1 = x\) and \(x + y = 3\)

\begin{align*} y + 1 &= x\\ y &= x - 1 \\ \therefore m_1 &= 1\\ x + y &= 3 \\ y &= -x + 3\\ \therefore m_2 &= - \\ \therefore m_1 & \ne m_2 \end{align*}

\(\therefore\)Not parallel lines.

The line passing through points \((-2;-1)\) and \((-4;-3)\) and the line \(-y + x - 4 = 0\)

\begin{align*} - y + x - 4 &= 0 \\ y &= x - 4 \\ \therefore m_1 &= 1 \\ m_2 &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{-3 + 1}{-4 + 2} \\ &= \frac{-2}{-2} \\ \therefore m_2 &= 1 \\ \therefore m_1 &= m_2 \end{align*}

\(\therefore\)Parallel lines.

\(y - 1 = \frac{1}{3}x\) and the line passing through points \((-2;4)\) and \((1;5)\)

\begin{align*} y - 1 &= \frac{1}{3}x \\ y &= \frac{1}{3}x + 1 \\ \therefore m_1 &= \frac{1}{3} \\ m_2 &= \frac{y_2 - y_1}{x_2 - x_1} \\ &= \frac{5 - 4}{1 + 2} \\ &= \frac{1}{3} \\ \therefore m_1 &= m_2 \end{align*}

\(\therefore\)Parallel lines.

Determine the equation of the straight line that passes through the point \((1;-5)\) and is parallel to the line \(y + 2x - 1 = 0\).

\begin{align*} y + 2x - 1 &= 0 \\ y &= -2x + 1 \\ \therefore m &= -2 \\ y - y_1&= m(x - x_1) \\ y + 5 &= -2(x - 1) \\ y &= -2x + 2 - 5 \\ \therefore y &= -2x - 3 \end{align*}

Determine the equation of the straight line that passes through the point \((-2;-6)\) and is parallel to the line \(2y + 1 = 6x\).

\begin{align*} 2y + 1 &= 6x \\ 2y &= 6x - 1 \\ y &= 3x - \frac{1}{2} \\ \therefore m &= 3 \\ y - y_1&= m(x - x_1) \\ y + 6 &= 3(x + 2) \\ y &= 3x + 6 - 6 \\ \therefore y &= 3x \end{align*}

Determine the equation of the straight line that passes through the point \((-2;-2)\) and is parallel to the line with angle of inclination \(\theta = \text{56,31}\text{°}\).

\begin{align*} \theta &= \text{56,31}\text{°} \\ \therefore m &= \tan \theta \\ &= \tan \text{56,31}\text{°} \\ \therefore m &= \text{1,5} \\ y - y_1&= m(x - x_1) \\ y + 2 &= \frac{3}{2}(x + 2) \\ y &= \frac{3}{2}x + 3 - 2 \\ \therefore y &= \frac{3}{2}x + 1 \end{align*}

Determine the equation of the straight line that passes through the point \((-2;\frac{2}{5})\) and is parallel to the line with angle of inclination \(\theta = \text{145}\text{°}\).

\begin{align*} \theta &= \text{145}\text{°} \\ \therefore m &= \tan \theta \\ &= \tan \text{145}\text{°} \\ \therefore m &= -\text{0,7} \\ y - y_1&= m(x - x_1) \\ y - \frac{2}{5} &= -\frac{7}{10}(x + 2) \\ y &= -\frac{7}{10}x - \frac{7}{5} + \frac{2}{5} \\ \therefore y &= -\frac{7}{10}x -1 \end{align*}

4.3 Inclination of a line

Table of Contents

4.5 Perpendicular lines