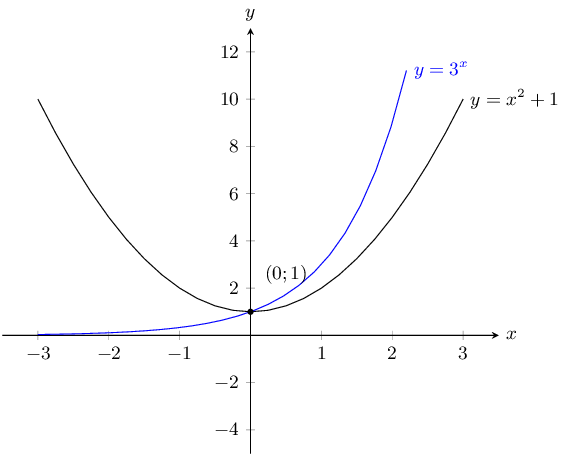
\(y = x^2 +1\) and \(y = 3^x\)
The \(y\)-intercept for each graph is:
\(\begin{aligned} 0^2 + 1 & = 1 \\ 3^0 & = 1 \end{aligned}\)This is also the only point of intersection.
For both graphs there is no \(x\)-intercept.

We think you are located in United States. Is this correct?
We use this information to present the correct curriculum and to personalise content to better meet the needs of our users.
|
Previous
6.6 Trigonometric functions
|
Next
6.8 Chapter summary
|
Use the sketch below to determine the values of \(a\) and \(q\) for the parabola of the form \(y=a{x}^{2}+q\).
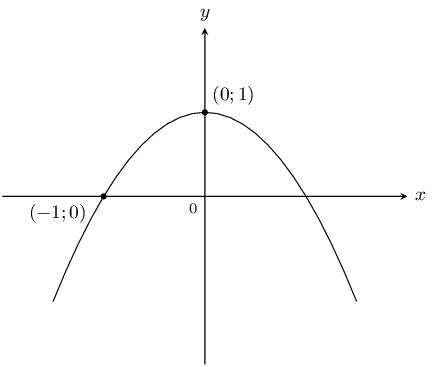
From the sketch we see that the shape of the graph is a “frown”, therefore \(a<0\). We also see that the graph has been shifted vertically upwards, therefore \(q>0\).
The \(y\)-intercept is the point \((0;1)\).
\begin{align*} y& = a{x}^{2}+q \\ 1& = a{(0)}^{2}+q \\ \therefore q& = 1 \end{align*}Substitute point \((-1;0)\) into the equation:
\begin{align*} y& = a{x}^{2}+q \\ 0& = a{(-1)}^{2}+1 \\ \therefore a& = -1 \end{align*}\(a=-1\) and \(q=1\), so the equation of the parabola is \(y=-{x}^{2}+1\).
Use the sketch below to determine the values of \(a\) and \(q\) for the hyperbola of the form \(y=\frac{a}{x}+q\).
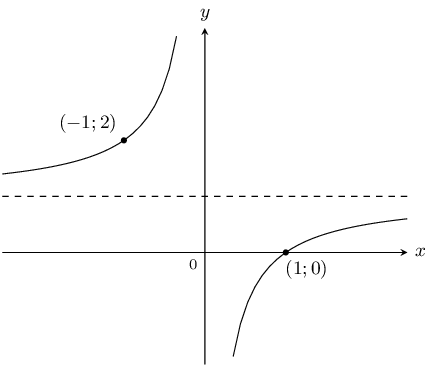
The two curves of the hyperbola lie in the second and fourth quadrant, therefore \(a<0\). We also see that the graph has been shifted vertically upwards, therefore \(q>0\).
Substitute the point \((-1;2)\):
\begin{align*} y& = \frac{a}{x}+q \\ 2& = \frac{a}{-1}+q \\ \therefore 2& = -a+q \end{align*}Substitute the point \((1;0)\):
\begin{align*} y& = \frac{a}{x}+q \\ 0& = \frac{a}{1}+q \\ \therefore a& = -q \end{align*}\(a=-1\) and \(q=1\), therefore the equation of the hyperbola is \(y=\dfrac{-1}{x}+1\).
The graphs of \(y=-{x}^{2}+4\) and \(y=x-2\) are given. Calculate the following:
coordinates of \(A\), \(B\), \(C\), \(D\)
coordinates of \(E\)
distance \(CD\)
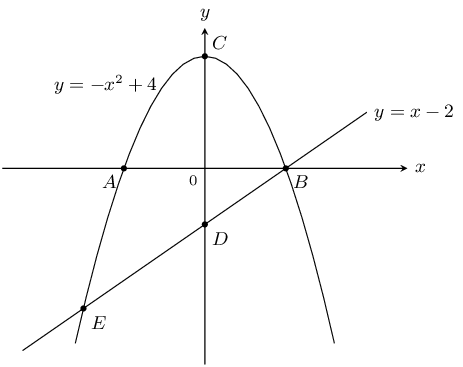
For the parabola, to calculate the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = -{x}^{2}+4 \\ & = -{0}^{2}+4 \\ & = 4 \end{align*}This gives the point \(C(0;4)\).
To calculate the \(x\)-intercept, let \(y=0\):
\begin{align*} y& = -{x}^{2}+4 \\ 0& = -{x}^{2}+4 \\ {x}^{2}-4& = 0 \\ (x+2)(x-2)& = 0 \\ \therefore x& = ±2 \end{align*}This gives the points \(A(-2;0)\) and \(B(2;0)\).
For the straight line, to calculate the \(y\)-intercept, let \(x=0\):
\begin{align*} y& = x-2 \\ & = 0-2 \\ & = -2 \end{align*}This gives the point \(D(0;-2)\).
At \(E\) the two graphs intersect so we can equate the two expressions:
\begin{align*} x-2& = -{x}^{2}+4 \\ \therefore {x}^{2}+x-6& = 0 \\ \therefore (x-2)(x+3)& = 0 \\ \therefore x& = 2 \text{ or } -3 \end{align*}At \(E\), \(x=-3\), therefore \(y=x-2=-3-2=-5\). This gives the point \(E(-3;-5)\).
Distance \(CD\) is \(\text{6}\) units.
coordinates of \(A(-2;0)\), \(B(2;0)\), \(C(0;4)\), \(D(0;-2)\)
coordinates of \(E(-3;-5)\)
distance \(CD = 6\) units
Use the sketch to determine the equation of the trigonometric function \(f\) of the form \(y=a f(\theta)+q\).
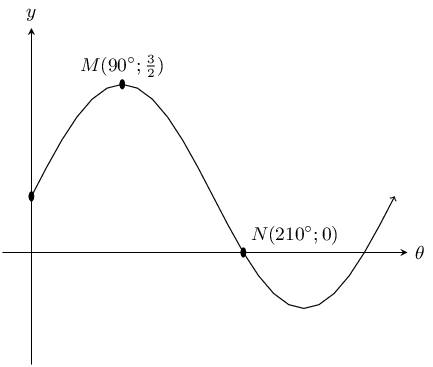
From the sketch we see that the graph is a sine graph that has been shifted vertically upwards. The general form of the equation is \(y=a\sin\theta +q\).
At \(N\), \(\theta =210°\) and \(y=0\):
\begin{align*} y& = a\sin\theta +q \\ 0& = a\sin 210°+q \\ & = a\left(-\frac{1}{2}\right)+q \\ \therefore q& = \frac{a}{2} \end{align*}At \(M\), \(\theta = 90°\) and \(y=\frac{3}{2}\):
\begin{align*} \frac{3}{2}& = a\sin90°+q \\ & = a+q \end{align*}Plot the following functions on the same set of axes and clearly label all the points at which the functions intersect.
\(y = x^2 +1\) and \(y = 3^x\)
The \(y\)-intercept for each graph is:
\(\begin{aligned} 0^2 + 1 & = 1 \\ 3^0 & = 1 \end{aligned}\)This is also the only point of intersection.
For both graphs there is no \(x\)-intercept.

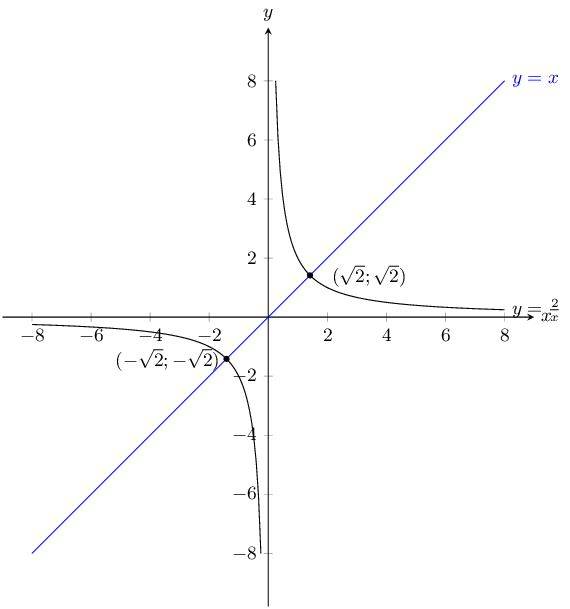
\(y = x\) and \(y = \dfrac{2}{x}\)
\(y = x\) is a basic straight line graph. For \(y =\frac{2}{x}\) there is no \(y\)-intercept and no \(x\)-intercept. We note that this is a hyperbolic graph that has been stretched by 2 units.
The points of intersection are:
\begin{align*} x &= \frac{2}{x} \\ x^2 &= 2 \\ x^2 - 2 & = 0\\ (x - \sqrt{2})(x + \sqrt{2}) & = 0\\ x = \sqrt{2} &\text{ or } x = -\sqrt{2} \\ y = \sqrt{2} &\text{ or } y = -\sqrt{2} \end{align*}The graphs intersect at \(\left(\sqrt{2};\sqrt{2}\right)\) and \(\left(-\sqrt{2};-\sqrt{2}\right)\).
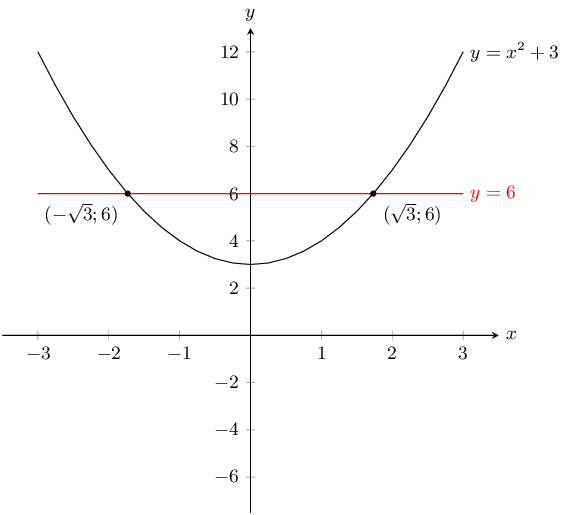
\(y = x^2 +3\) and \(y = 6\)
\(y = 6\) is a horizontal line through \((0;6)\). For \(y =x^2 + 3\) the \(y\)-intercept is \((0;3)\) and there are no \(x\)-intercepts. From the value of \(q\) we see that this is a basic parabola that has been shifted upwards by 3 units.
The points of intersection are:
\begin{align*} x^2 + 3 &= 6 \\ x^2 - 3 &= 0 \\ (x - \sqrt{3})(x + \sqrt{3}) & = 0\\ x = \sqrt{3} &\text{ or } x = -\sqrt{3} \\ y = 6 \end{align*}The graphs intersect at \(\left(\sqrt{3};6\right)\) and \(\left(-\sqrt{3};-6\right)\).
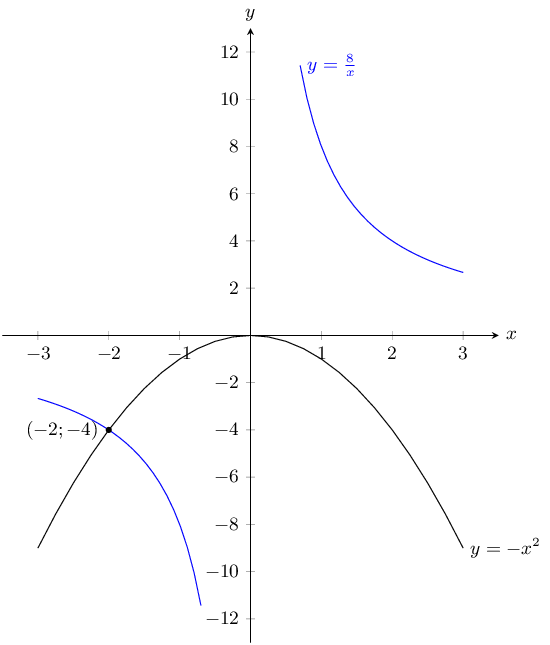
\(y = -x^2\) and \(y = \dfrac{8}{x}\)
\(y = -x^{2}\) is a parabola that has been reflected about the \(x\)-axis. For \(y =\frac{8}{x}\) there is no \(y\)-intercept and there is no \(x\)-intercepts. From the value of \(a\) we see that this is a basic hyperbola that has been stretched by 8 units.
The points of intersection are:
\begin{align*} -x^2 &= \frac{8}{x} \\ x^3 &= - 8 \\ x & = -2\\ y &= \frac{8}{-2} \\ y &= -4 \end{align*}The graphs intersect at \(\left(-2;-4\right)\).
Determine the equations for the graphs given below.

For the straight line graph we have the \(x\) and \(y\)-intercepts. The \(y\)-intercept gives \(c = 2\). Now we can calculate the gradient of the straight line graph:
\begin{align*} y &= mx + 2 \\ m &= \frac{2 - 0}{0 - (-2)} \\ &= 1 \end{align*}Therefore the equation of the straight line graph is \(y = x + 2\).
For the parabola we also have the \(x\) and \(y\)-intercepts. The \(y\)-intercept gives \(q = 2\). Now we can calculate \(a\):
\begin{align*} y &= ax^2 + 2 \\ 0 &= a(-2)^2 + 2 \\ -2 &= 4a \\ a &= -\frac{1}{2} \end{align*}Therefore the equation of the parabola is \(y = -\frac{1}{2}x^2 + 2\).
The equations for the two graphs are \(y = x + 2\) and \(y = -\frac{1}{2}x^2 + 2\)

For the straight line graph we notice that it passes through \((0;0)\) and so \(c = 0\).
We have two points on the straight line graph and so we can calculate the gradient, \(m\):
\begin{align*} y &= mx + 0 \\ m &= \frac{8 - (-8)}{1 - (- 1)} \\ m &= 8 \end{align*}The equation of the straight line graph is \(y = 8x\).
For the hyperbola we note that the graph is not shifted either upwards or downwards. Therefore \(q = 0\). Now we can calculate \(a\):
\begin{align*} y &= \frac{a}{x} \\ 8 &= \frac{a}{1} \\ a &= 8 \end{align*}Therefore the equation of the hyperbola is \(y = \frac{8}{x}\).
The equations for the two graphs are \(y = 8x\) and \(y = \frac{8}{x}\).
Choose the correct answer:
The range of \(y = 2 \sin{\theta} + 1\) is:
3
The range of \(y = 2 \cos{\theta} - 4\) is:
4
The y-intercept of \(2^x + 1\) is:
3
Which of the following passes through \((1;7)\)?
1
|
Previous
6.6 Trigonometric functions
|
Table of Contents |
Next
6.8 Chapter summary
|