8.7 Summary (EMCJJ)

• A ratio describes the relationship between two quantities which have the same units.

  $$x:y \quad \text{ or } \quad \frac{x}{y} \quad \text{ or } \quad x \enspace \text{ to } \enspace y$$

• If two or more ratios are equal to each other $\left( \frac{m}{n} = \frac{p}{q} \right)$, then $m$ and $n$ are in the same proportion as $p$ and $q$.

• A polygon is a plane, closed shape consisting of three or more line segments.

• Triangles with equal heights have areas which are proportional to their bases.

• Triangles with equal bases and between the same parallel lines are equal in area.

• Triangles on the same side of the same base and equal in area lie between parallel lines.

• A line drawn parallel to one side of a triangle divides the other two sides of the triangle in the same proportion.

  

• Converse: proportion theorem

  If a line divides two sides of a triangle in the same proportion, then the line is parallel to the third side.

• Special case: the mid-point theorem

  The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half the length of the third side.

  If $AB = BD$ and $AC = CE$, then $BC \parallel DE$ and $BC = \frac{1}{2}DE$.

  

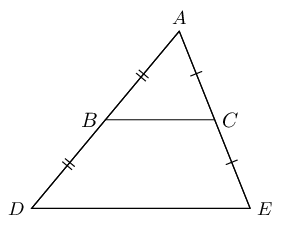
• Converse: the mid-point theorem

  The line drawn from the mid-point of one side of a triangle parallel to another side, bisects the third side of the triangle.

  If $AB = BD$ and $BC \parallel DE$, then $AC = CE$.

• Polygons are similar if they are the same shape but differ in size. One polygon is an enlargement of the other.

• Two polygons with the same number of sides are similar when:

  1. All pairs of corresponding angles are equal, and
  2. All pairs of corresponding sides are in the same proportion.

• If two triangles are equiangular, then the triangles similar.

  

• Triangles with sides in proportion are equiangular and therefore similar.

  

• The square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides.

  

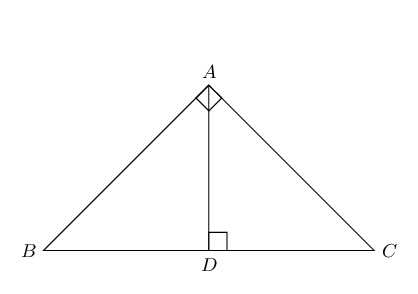
• Converse: theorem of Pythagoras

  If the square of one side of a triangle is equal to the sum of the squares of the other two sides of the triangle, then the angle included by these two sides is a right angle.