Chapter 5: Addition and subtraction of integers

Chapter 6: Operations with fractions

6.1 Addition and subtraction of fractions

In Chapter 4, you learnt that a common fraction is written as two whole numbers, one on top of the other: $\frac{\text{numerator}}{\text{denominator}}$ .

The denominator represents all the parts of a whole. For example, in the fraction $\frac{2}{7}$ , each whole is divided into 7 parts.
The numerator represents only the parts of a whole we are dealing with. For example, in the fraction $\frac{2}{7}$ , we are dealing with only 2 out of 7 parts.

Adding fractions with the same denominator

Usman and Adamu are at a birthday party. There is a cake that is cut into 4 pieces:

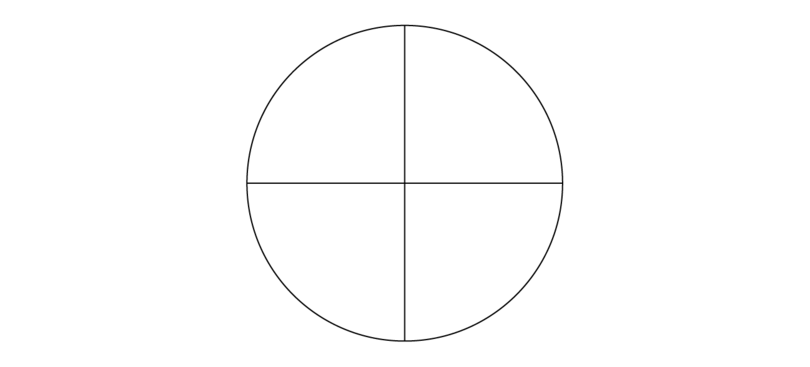
Suppose Usman gets $\frac{1}{4}$ of the cake:

Suppose Adamu also gets $\frac{1}{4}$ of the cake:

If they put their pieces of cake together, they have $\frac{2}{4}$ of the cake:

We write this as:

$\frac{1}{4}+\frac{1}{4}=\frac{2}{4}$

Remember that the denominator of a fraction tells us into how many parts a whole is divided. In this case, one whole cake is divided into 4 pieces. Together, the boys have 2 of those pieces.

In Chapter 4, you learnt how to write a fraction in its simplest form. This is when the numerator and denominator have no common factor.

The simplest form of $\frac{2}{4}$ is $\frac{1}{2}$ .

We may therefore write:

$\frac{1}{4}+\frac{1}{4}=\frac{1}{2}$

Subtracting fractions with the same denominator

Suppose another cake arrives at the birthday party that Usman and Adamu are attending. This cake is also cut into 4 pieces. Someone immediately takes a piece, so that only 3 of the 4 pieces are left. The cake may now be represented as follows.

There is $\frac{3}{4}$ of the cake left:

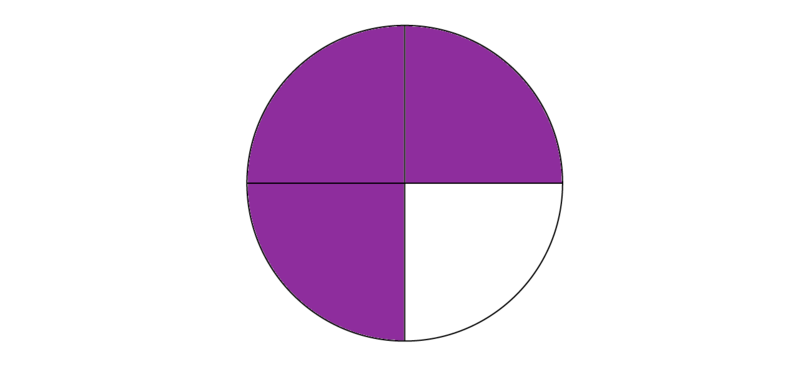
Danladi did not have any cake yet. He gets 1 piece, which is $\frac{1}{4}$ of the cake:

After Danladi took his piece, $\frac{2}{4}$ of the cake is left:

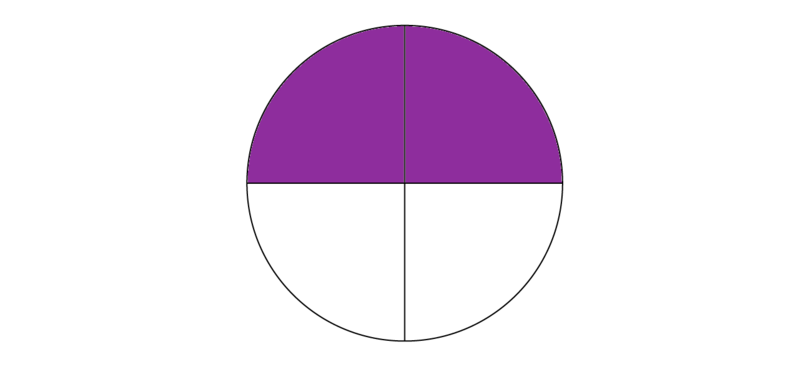
We write this as:

$\frac{3}{4}-\frac{1}{4}=\frac{2}{4}$

The simplest form of $\frac{2}{4}$ is $\frac{1}{2}$ .

We may therefore write:

$\frac{3}{4}-\frac{1}{4}=\frac{1}{2}$

Worked example 6.1: Adding fractions with the same denominator

Calculate:
$\frac{7}{10}+\frac{1}{10}$

Method 1 (Using diagrams)

1. The denominator shows into how many parts one whole must be divided. Represent this in a diagram. In this case, there must be 10 parts.

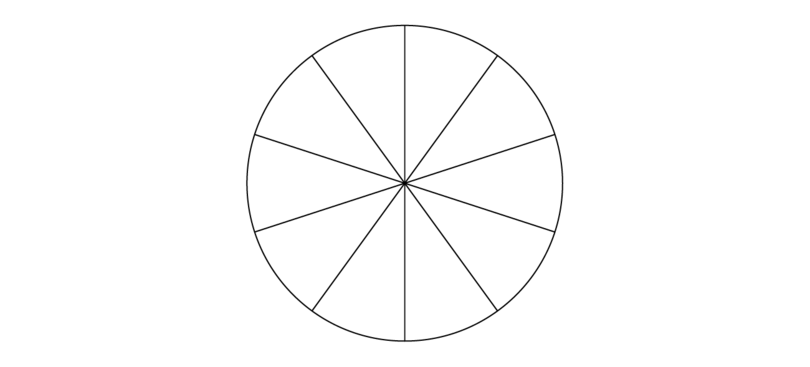
2. Shade the number of parts shown by the first numerator. The first numerator is 7.

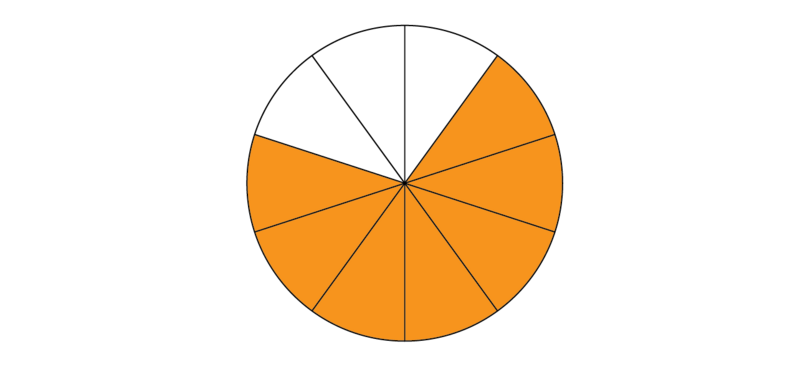
3. Now also shade the number of parts shown by the second numerator. The second numerator is 1. We must shade another 1 part.

4. Write the total shaded part as a fraction:
$\frac{8}{10}$
5. Write the fraction in its simplest form.
$\frac{8\div 2}{10\div 2}=\frac{4}{5}$
6. The full calculation is:
$\begin{array}{l} \phantom{00}\frac{7}{10}+\frac{1}{10}\newline =\frac{8}{10} \newline =\frac{4}{5} \end{array}$
Method 2 (Calculating directly)

1. The denominator shows into how many parts one whole must be divided. Write down the denominator.
$\begin{array}{l} \phantom{00}\frac{7}{10}+\frac{1}{10}\newline =\frac{\phantom{00000}}{10} \newline \end{array}$
2. Write down the numerators that must be added.
$\begin{array}{l} \phantom{00}\frac{7}{10}+\frac{1}{10}\newline =\frac{7+1}{10} \newline \end{array}$
3. Add the numerators.
$\begin{array}{l} \phantom{00}\frac{7}{10}+\frac{1}{10}\newline =\frac{7+1}{10} \newline =\frac{8}{10} \newline \end{array}$
4. Simplify the answer.
$\begin{array}{l} \phantom{00}\frac{7}{10}+\frac{1}{10}\newline =\frac{7+1}{10} \newline =\frac{8}{10} \newline =\frac{4}{5} \end{array}$

Worked example 6.2: Subtracting fractions with the same denominator

Calculate:
$\frac{7}{9}-\frac{3}{9}$

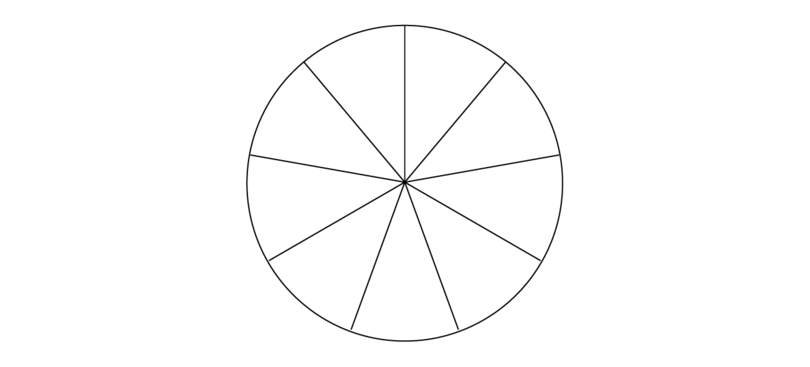
Method 1: Using diagrams

1. The denominator shows into how many parts one whole must be divided. Represent this in a diagram. In this case, there must be 9 parts.

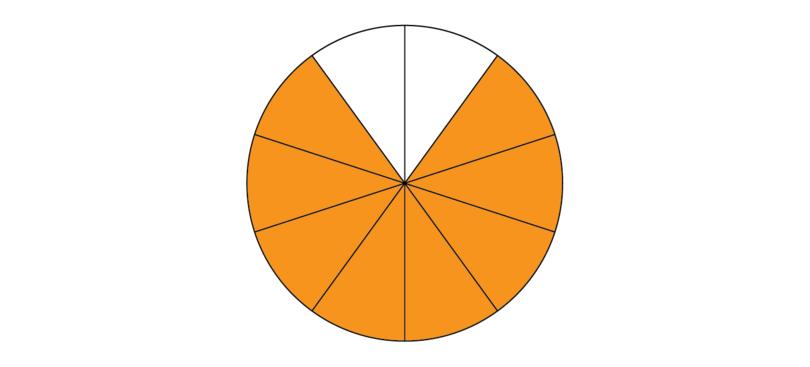
2. Shade the number of parts shown by the first numerator. The first numerator is 7.

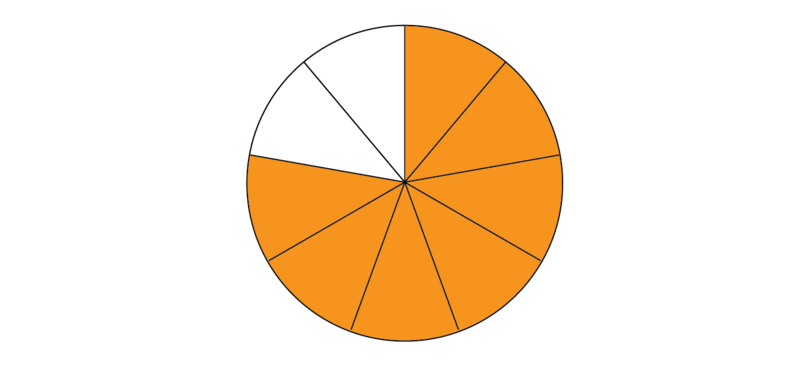
3. Scratch out the number of parts shown by the numerator that is subtracted. The second numerator is 3. We must scratch out 3 parts.

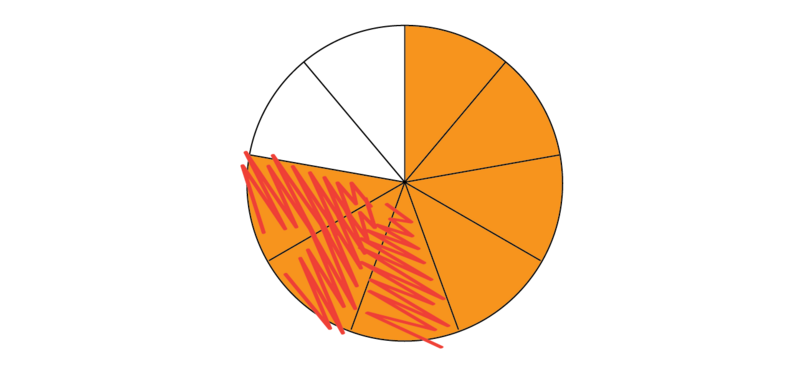
4. Redraw the diagram, shading only the parts that are left over. There are 4 parts left over.

5. Write the shaded part as a fraction.
$\frac{4}{9}$
6. Check whether the fraction is in its simplest form.

In this case, the numerator and denominator have no common factors.

7. The full calculation is:
$\begin{array}{l} \phantom{00}\frac{7}{9}-\frac{3}{9}\newline =\frac{4}{9} \newline \end{array}$
Method 2: Calculating directly

1. The denominator shows into how many parts one whole must be divided. Write down the denominator.
$\begin{array}{l} \phantom{00}\frac{7}{9}-\frac{3}{9}\newline =\frac{\phantom{0000}}{9} \newline \end{array}$
2. Write down the numerators that must be subtracted.
$\begin{array}{l} \phantom{00}\frac{7}{9}-\frac{3}{9}\newline =\frac{7-3}{9} \newline \end{array}$
3. Subtract the numerators.
$\begin{array}{l} \phantom{00}\frac{7}{9}-\frac{3}{9}\newline =\frac{7-3}{9} \newline =\frac{4}{9} \newline \end{array}$
4. Simplify the answer if necessary. In this case, is it not necessary.

Exercise 6.1: Add and subtract fractions that have the same denominators

Calculate each of the following.

$\frac{3}{11}+\frac{5}{11}$
$\begin{array}{l} \phantom{00}\frac{3}{11}+\frac{5}{11}\newline =\frac{3+5}{11} \newline =\frac{8}{11} \newline \end{array}$
$\frac{7}{12}+\frac{3}{12}$
$\begin{array}{l} \phantom{00}\frac{7}{12}+\frac{3}{12}\newline =\frac{7+3}{12} \newline =\frac{10}{12} \newline =\frac{5}{6} \end{array}$
$\frac{11}{36}+\frac{13}{36}$
$\begin{array}{l} \phantom{00}\frac{11}{36}+\frac{13}{36}\newline =\frac{11+13}{36} \newline =\frac{24}{36} \newline =\frac{2}{3} \end{array}$
$\frac{15}{17}-\frac{9}{17}$
$\begin{array}{l} \phantom{00}\frac{15}{17}-\frac{9}{17}\newline =\frac{15-9}{17} \newline =\frac{6}{17} \newline \end{array}$
$\frac{19}{20}-\frac{7}{20}$
$\begin{array}{l} \phantom{00}\frac{19}{20}-\frac{7}{20}\newline =\frac{19-7}{20} \newline =\frac{12}{20} \newline =\frac{3}{5} \end{array}$
$\frac{41}{48}-\frac{5}{48}$
$\begin{array}{l} \phantom{00}\frac{41}{48}-\frac{5}{48}\newline =\frac{41-5}{48} \newline =\frac{36}{48} \newline =\frac{3}{4} \end{array}$

Adding and subtracting fractions with different denominators

Suppose we want to determine the following:

$\frac{2}{3}+\frac{1}{2}$
$\frac{2}{3}-\frac{1}{2}$

$\frac{2}{3}$ of a cake may be represented as:

$\frac{1}{2}$ of a cake may be represented as:

We can divide one cake into either 2 pieces or 3 pieces. We cannot divide the cake into both. To overcome this problem, we have to express both fractions with the same denominator. The lowest common denominator (LCD) of 2 and 3 is 6. The equivalent fractions of $\frac{2}{3}$ and $\frac{1}{2}$ , with 6 as their denominator, are:

$\frac{2}{3}=\frac{2\times2}{3\times2}=\frac{4}{6}$

$\frac{1}{2}=\frac{1\times3}{2\times3}=\frac{3}{6}$

Now we can follow the same method as before.

If necessary, go back to Chapter 4 for information about the lowest common denominator (LCD) of two or more fractions. Revise how find equivalent fractions that all have the LCD as their denominator.

Worked example 6.3: Adding fractions with different denominators

Calculate:
$\frac{2}{3}+\frac{1}{2}$

Step 1: Compare the denominators. If they are different, find the LCD.

The LCD of 2 and 3 is 6.
Step 2: Find equivalent fractions with the LCD as their denominators.
$\frac{2}{3}=\frac{4}{6}$ $\frac{1}{2}=\frac{3}{6}$
Step 3: Use the LCD to represent the parts of one whole in a diagram.

In this case, there must be 6 parts.
Step 4: Shade the number of parts shown by the first numerator of the equivalent fraction.

This is 4.
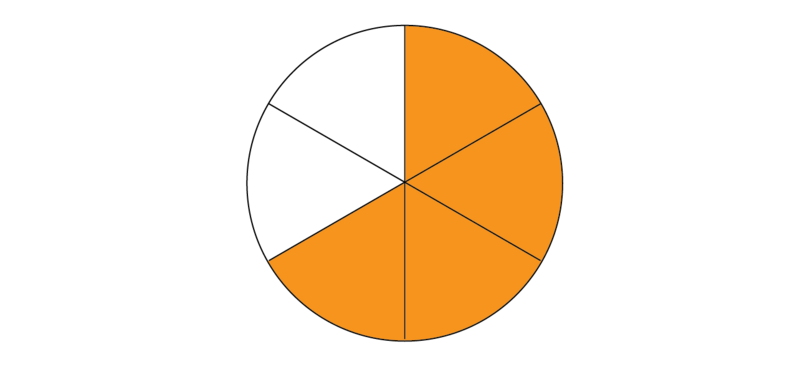
Step 5: Shade the additional parts shown by the second numerator of the equivalent fraction.

The second numerator is 3. We must shade another 3 parts.

There are only 2 "gaps" in the shape that can be shaded. Therefore, we need to add another shape.
Step 6: Write the total shaded part as a fraction.

The fraction is $\frac{7}{6}$ .

Remember, the denominator shows into how many parts one whole is divided. The numerator shows the total number of those parts that we are dealing with.
Step 7: Write the answer in its simplest form or as a mixed number.
$\frac{7}{6}=1\frac{1}{6}$
Step 8: Write out the whole calculation.
$\begin{array}{l} \phantom{00}\frac{2}{3}+\frac{1}{2}\newline =\frac{4}{6}+\frac{3}{6}\newline =\frac{4+3}{6} \newline =\frac{7}{6} \newline =1\frac{1}{6} \end{array}$

Worked example 6.4: Subtracting fractions with different denominators

Calculate:
$\frac{2}{3}-\frac{1}{2}$

Step 1: Compare the denominators. If they are different, find the LCD.

The LCD of 2 and 3 is 6.
Step 2: Find equivalent fractions with the LCD as their denominators.
$\frac{2}{3}=\frac{4}{6}$ $\frac{1}{2}=\frac{3}{6}$
Step 3: Use the LCD to represent the parts of one whole in a diagram.

In this case, there must be 6 parts.
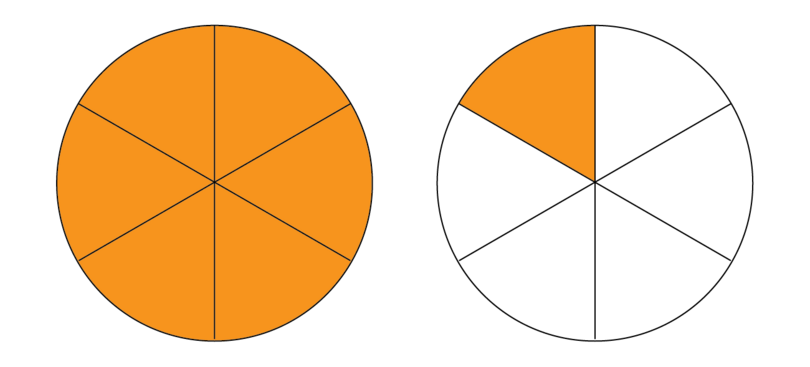
Step 4: Shade the number of parts shown by the first numerator of the equivalent fraction.

This is 4.
Step 5: Scratch out the number of parts shown by the numerator of the equivalent fraction that is subtracted. Then redraw the diagram with only the parts that are left over shaded.

The second numerator is 3. We must scratch out 3 parts.

There is only one part left over.
Step 6: Write the shaded part as a fraction.
$\frac{1}{6}$
Step 7: Check whether the fraction is in its simplest form.

In this case, the numerator and denominator have no common factors.
Step 8: Write out the whole calculation.
$\begin{array}{l} \phantom{00}\frac{2}{3}-\frac{1}{2}\newline =\frac{4}{6}-\frac{3}{6}\newline =\frac{4-3}{6} \newline =\frac{1}{6} \end{array}$

As you get used to adding and subtracting fractions, it will no longer be necessary to draw diagrams. Just be sure to always write out the calculation in full.

Exercise 6.2: Add and subtract fractions that have different denominators

Calculate each of the following.

$\frac{3}{4}+\frac{1}{8}$

LCD = 8
$\begin{array}{l} \phantom{00}\frac{3}{4}+\frac{5}{8}\newline =\frac{6}{8}+\frac{1}{8} \newline =\frac{6+1}{8} \newline =\frac{7}{8} \end{array}$
$\frac{2}{3}+\frac{2}{7}$

LCD = 21
$\begin{array}{l} \phantom{00}\frac{2}{3}+\frac{2}{7}\newline =\frac{14}{21}+\frac{6}{21} \newline =\frac{14+6}{21} \newline =\frac{20}{21} \end{array}$
$\frac{11}{30}+\frac{4}{12}$

$30=2\times3\times5$
$12=2^2\times3$
$\text{LCD} = 2^2\times3\times5= 60$
$\begin{array}{l} \phantom{00}\frac{11}{30}+\frac{4}{12}\newline =\frac{22}{60}+\frac{20}{60} \newline =\frac{22+20}{60} \newline =\frac{42}{60} \newline =\frac{7}{10} \end{array}$
$\frac{10}{15}+\frac{8}{20}$

$15=3\times5$
$20=2^2\times5$
$\text{LCD} = 2^2\times3\times5= 60$
$\begin{array}{l} \phantom{00}\frac{10}{15}+\frac{8}{20}\newline =\frac{40}{60}+\frac{24}{60} \newline =\frac{40+24}{60} \newline =\frac{64}{60} \newline =\frac{16}{15}\newline =1\frac{1}{15} \end{array}$
$\frac{1}{8}+\frac{5}{6}+\frac{5}{10}$

$8=2^3$
$6=2\times3$
$10=2\times5$
$\text{LCD} = 2^3\times3\times5= 120$
$\begin{array}{l} \phantom{00}\frac{1}{8}+\frac{5}{6}+\frac{5}{10}\newline =\frac{15}{120}+\frac{100}{120}+\frac{60}{120} \newline =\frac{15+100+60}{120} \newline =\frac{175}{120} \newline =\frac{35}{24}\newline =1\frac{11}{24} \end{array}$
$\frac{11}{15}-\frac{3}{5}$

LCD = 15
$\begin{array}{l} \phantom{00}\frac{11}{15}-\frac{3}{5}\newline =\frac{11}{15}-\frac{9}{15}\newline =\frac{11-9}{15} \newline =\frac{2}{15} \end{array}$
$\frac{5}{6}-\frac{2}{5}$

LCD = 30
$\begin{array}{l} \phantom{00}\frac{5}{6}-\frac{2}{5}\newline =\frac{25}{30}-\frac{12}{30}\newline =\frac{25-12}{30} \newline =\frac{13}{30} \end{array}$
$\frac{9}{12}-\frac{3}{15}$

$12=2^2\times3$
$15=3\times5$
$\text{LCD} = 2^2\times3\times5= 60$
$\begin{array}{l} \phantom{00}\frac{9}{12}-\frac{3}{15}\newline =\frac{45}{60}-\frac{12}{60}\newline =\frac{45-12}{60} \newline =\frac{33}{60} \newline =\frac{11}{20} \end{array}$
$\frac{23}{24}-\frac{12}{18}$

$24=2^3\times3$
$18=2\times3^2$
$\text{LCD} = 2^3\times3^2= 72$
$\begin{array}{l} \phantom{00}\frac{23}{24}-\frac{12}{18}\newline =\frac{69}{72}-\frac{48}{72}\newline =\frac{69-48}{72} \newline =\frac{21}{72} \newline =\frac{7}{24} \end{array}$
$\frac{9}{10}-\frac{1}{6}-\frac{2}{15}$

$10=2\times5$
$6=2\times3$
$15=3\times5$
$\text{LCD} = 2\times3\times5= 30$
$\begin{array}{l} \phantom{00}\frac{9}{10}-\frac{1}{6}-\frac{2}{15}\newline =\frac{27}{30}-\frac{5}{30}-\frac{4}{30} \newline =\frac{27-5-4}{30} \newline =\frac{18}{30} \newline =\frac{3}{5} \end{array}$

Adding and subtracting mixed numbers

Remember that a mixed number is made up of a whole number and a proper fraction. There are various methods that may be used to add and subtract mixed numbers. It is recommended that you first convert all mixed numbers to improper fractions before you add or subtract.

If necessary, go back to Chapter 4 and revise how to convert mixed numbers to improper fractions.

Worked example 6.5: Adding mixed numbers

Calculate:
$2\frac{4}{5}+1\frac{2}{3}$

Step 1: Convert the mixed numbers to improper fractions.
$2\frac{4}{5}=\frac{(2\times5)+4}{5}=\frac{14}{5}$ $1\frac{2}{3}=\frac{(1\times3)+2}{3}=\frac{5}{3}$
Step 2: If the denominators differ, find equivalent fractions with the LCD as their denominators.

The LCD of 3 and 5 is 15.
$\frac{14}{5}=\frac{42}{15}$ $\frac{5}{3}=\frac{25}{15}$
Step 3: Write down the LCD and add the numerators of the equivalent fractions.
$\begin{array}{l} \phantom{00}\frac{42}{15}+\frac{25}{15}\newline =\frac{42+25}{15} \newline =\frac{67}{15} \end{array}$
Step 4: Simplify the answer by converting the improper fraction to a mixed number.
$\begin{array}{l} \phantom{00}\frac{42}{15}+\frac{25}{15}\newline =\frac{42+25}{15} \newline =\frac{67}{15} \newline =4\frac{7}{15} \newline \end{array}$

Exercise 6.3: Add and subtract mixed numbers

Calculate each of the following.

$2\frac{1}{6}+1\frac{3}{8}$
$2\frac{1}{6}=\frac{13}{6}$ $1\frac{3}{8}=\frac{11}{8}$
$6=2\times3$
$8=2^3$
$\text{LCD} = 2^3\times3= 24$
$\begin{array}{l} \phantom{00}\frac{13}{6}+\frac{11}{8}\newline =\frac{52}{24}+\frac{33}{24} \newline =\frac{52+33}{24} \newline =\frac{85}{24} \newline =3\frac{13}{24} \end{array}$
$2\frac{5}{12}-1\frac{3}{28}$
$2\frac{5}{12}=\frac{29}{12}$ $1\frac{3}{28}=\frac{31}{28}$
$12=2^2\times3$
$28=2^2\times7$
$\text{LCD} = 2^2\times3\times7= 84$
$\begin{array}{l} \phantom{00}\frac{29}{12}-\frac{31}{28}\newline =\frac{203}{84}+\frac{93}{84} \newline =\frac{203-93}{84} \newline =\frac{110}{84} \newline =\frac{55}{42}\newline =1 \frac{13}{42} \end{array}$
$1\frac{7}{8}+2\frac{3}{10}-3\frac{1}{20}$
$1\frac{7}{8}=\frac{15}{8}$ $2\frac{3}{10}=\frac{23}{10}$ $3\frac{1}{20}=\frac{61}{20}$
$8=2^3$
$10=2\times5$
$20=2^2\times5$
$\text{LCD} = 2^3\times5= 40$
$\begin{array}{l} \phantom{00}\frac{15}{8}+\frac{23}{10}-\frac{61}{20}\newline =\frac{75}{40}+\frac{92}{40}-\frac{122}{40} \newline =\frac{75+92-122}{40} \newline =\frac{45}{40} \newline =\frac{9}{8}\newline =1 \frac{1}{8} \end{array}$

6.2 Multiplication and division of fractions

Multiplication: whole number x fraction

You might remember from previous years that multiplication is a form of addition. For example, $5 \times \triangle$ means $\triangle + \triangle + \triangle + \triangle + \triangle$ .

In the same way, $5\times\frac{1}{4}$ means $\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ .

Worked example 6.6: Multiplying: whole number x fraction

Calculate:
$5\times\frac{1}{4}$

Step 1: Write the multiplication as an addition.
$5\times\frac{1}{4}=\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$
Step 2: The denominator shows into how many parts one whole must be divided. Represent this in a diagram.

In this case, there must be 4 parts.
Step 3: Shade the number of parts shown by the first numerator.

This is 1.
Step 4: Shade the number of parts shown by the rest of the numerators.

We must shade another $1+1+1+1$ parts.

There are only 3 "gaps" in the shape that can be shaded. Therefore, we need to add another shape.
Step 6: Write the total shaded part as a fraction.

The fraction is $\frac{5}{4}$ .

Remember, the denominator shows into how many parts one whole is divided. The numerator shows the total number of those parts that we are dealing with.
Step 7: Write the answer in its simplest form or as a mixed number.
$\frac{5}{4}=1\frac{1}{4}$
Step 8: Write out the whole calculation.
$\begin{array}{l} \phantom{00}\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}\newline =\frac{1+1+1+1+1}{4} \newline =\frac{5}{4} \newline =1\frac{1}{4} \end{array}$
Note the numerator: $1+1+1+1+1=5\times1$

Multiplication: fraction x whole number

By now you know that $\frac{2}{5}$ of a cake may be represented as follows:

Suppose Azubuike ate $\frac{2}{5}$ of 3 cakes. How much cake did he actually eat? We must multiply $\frac{2}{5}$ by 3 cakes: $\frac{2}{5}\times3$ .

Worked example 6.7: Multiplying: fraction x whole number

Calculate:
$\frac{2}{5}\times3$

Step 1: Use a diagram to represent the fraction.

The fraction is $\frac{2}{5}$ .
Step 2: Add diagrams as required by the whole number.

The whole number is 3. This means we have $\frac{2}{5}+\frac{2}{5}+\frac{2}{5}$ .
Step 3: Put all the shaded parts together into one shape as far as possible, and then start using the next shape you need.
Step 4: Write the total shaded part as a fraction.

The fraction is $\frac{6}{5}$ .

Remember, the denominator shows into how many parts one whole is divided. The numerator shows the total number of those parts that we are dealing with.
Step 5: Write the answer in its simplest form or as a mixed number.
$\frac{6}{5}=1\frac{1}{5}$
Step 8: Write out the whole calculation.
$\begin{array}{l} \phantom{00}\frac{2}{5}+\frac{2}{5}+\frac{2}{5}\newline =\frac{2+2+2}{5} \newline =\frac{6}{5} \newline =1\frac{1}{5} \end{array}$
Note the numerator: $2+2+2=3\times2$

Exercise 6.4: Multiply fractions and whole numbers

Calculate each of the following.

$4\times\frac{6}{9}$
$\begin{array}{l} \phantom{00}4\times\frac{6}{9}\newline =\frac{6}{9}+\frac{6}{9}+\frac{6}{9}+\frac{6}{9} \newline =\frac{6+6+6+6}{9} \newline =\frac{24}{9} \newline =\frac{8}{3}\newline =2\frac{2}{3} \end{array}$
$6\times\frac{3}{10}$
$\begin{array}{l} \phantom{00}6\times\frac{3}{10}\newline =\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10}+\frac{3}{10} \newline =\frac{3+3+3+3+3+3}{10} \newline =\frac{18}{10} \newline =\frac{9}{5}\newline =1\frac{4}{5} \end{array}$
$\frac{3}{8}\times5$
$\begin{array}{l} \phantom{00}\frac{3}{8}\times5\newline =\frac{3}{8}+\frac{3}{8}+\frac{3}{8}+\frac{3}{8}+\frac{3}{8} \newline =\frac{3+3+3+3+3}{8} \newline =\frac{15}{8} \newline =1\frac{7}{8} \end{array}$
$\frac{9}{14}\times4$
$\begin{array}{l} \phantom{00}\frac{9}{14}\times4\newline =\frac{9}{14}+\frac{9}{14}+\frac{9}{14}+\frac{9}{14} \newline =\frac{9+9+9+9}{14} \newline =\frac{36}{14} \newline =\frac{18}{7}\newline =2\frac{4}{7} \end{array}$

Once you understand how to multiply whole numbers and fractions, you may use this short method.
Example: $\frac{2}{7}\times6$
Denominator (stays the same): $\frac{\phantom{00}}{7}$
Numerator: $2\times6=12$
Calculation:
$\begin{array}{l} \phantom{00}\frac{2}{7}\times6\newline =\frac{2\times6}{7} \newline =\frac{12}{7}\newline =1\frac{5}{7} \end{array}$

Multiplication: fraction x fraction

When we write $\frac{2}{3}\times\frac{3}{4}$ , it means two thirds, $\frac{2}{3}$ , of three quarters, $\frac{3}{4}$ .

By now you know that $\frac{3}{4}$ of a cake may be represented as follows:

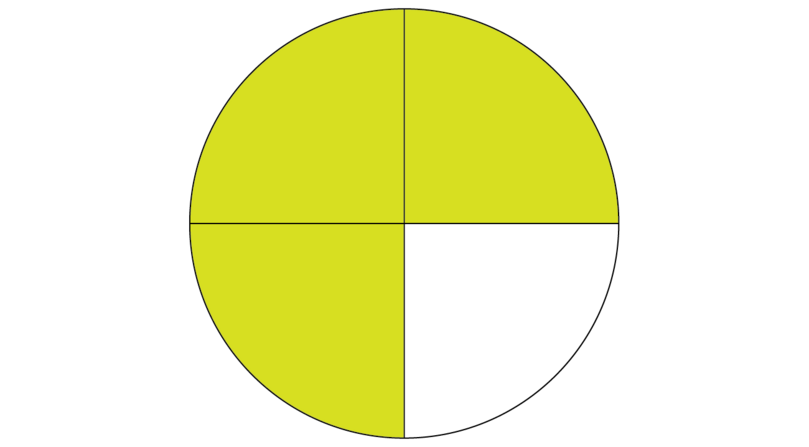
Now we want to know how much $\frac{2}{3}$ of the shaded part is.

Worked example 6.8: Multiplying using a diagram: fraction x fraction

Calculate:
$\frac{2}{3}\times\frac{3}{4}$

Step 1: Use a diagram to represent one of the fractions.
Step 2: Divide the shape further, according to the denominator of the other fraction.

The denominator of $\frac{2}{3}$ is 3. This means we must divide each part of the shape further into 3 parts.
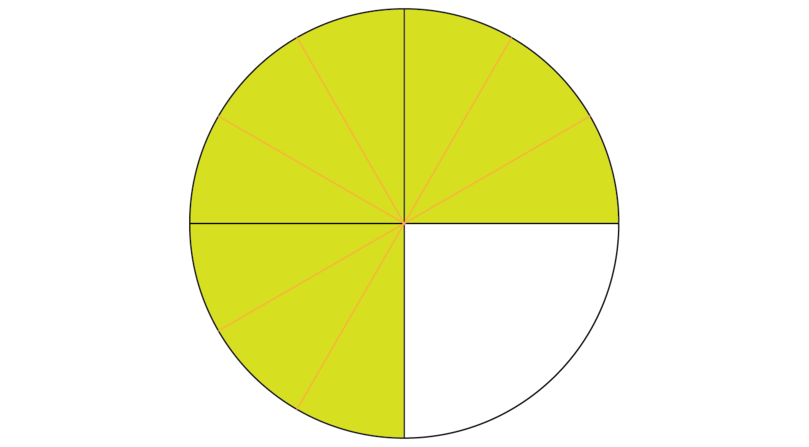
Step 3: Use another colour to shade the correct portion of the shaded part, according to the numerator of the fraction used in Step 2.

The numerator of $\frac{2}{3}$ is 2. This means that we are interested in 2 of every 3 parts. Remember that we only want $\frac{2}{3}$ of the part that is already shaded, $\frac{3}{4}$ .
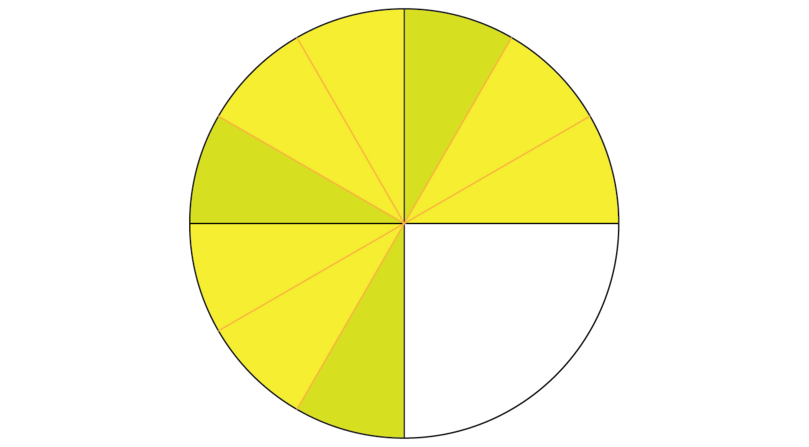
Step 4: Write the newly shaded part as a fraction of the whole shape.

Remember, the shape is now divided into 12 parts. The new shading covers 6 of those parts.

The fraction is $\frac{6}{12}$ .
Step 5: Write the answer in its simplest form or as a mixed number.
$\frac{6}{12}=\frac{1}{2}$
Step 6: Write out the whole calculation.
$\begin{array}{l} \phantom{00}\frac{2}{3}\times\frac{3}{4}\newline =\frac{6}{12} \newline =\frac{1}{2} \newline \end{array}$
If you use the same method to determine $\frac{3}{4}\times\frac{2}{3}$ , you will get the same answer.

See whether you notice a pattern when we write the first two lines of the calculation in Step 6 of the previous worked example as follows:

$\frac{2}{3}\times\frac{3}{4}=\frac{6}{12}$

When we multiply two fractions, we may follow this method:

$\frac{\text{numerator 1}}{\text{denominator 1}}\times\frac{\text{numerator 2}}{\text{denominator 2}}=\frac{\text{numerator 1}\times\text{numerator 2}}{\text{denominator 1}\times\text{denominator 2}}$

Worked example 6.9: Calculating fraction x fraction directly

Calculate:
$\frac{5}{6}\times\frac{3}{8}$

Step 1: Multiply the two numerators and multiply the two denominators.
$\frac{5}{6}\times\frac{3}{8}=\frac{5\times3}{6\times8}$
Step 2: Find the numerator and denominator of the answer.
$\frac{5}{6}\times\frac{3}{8}=\frac{5\times3}{6\times8}=\frac{15}{48}$
Step 3: Write the answer in its simplest form or as a mixed number.
$\frac{5}{6}\times\frac{3}{8}=\frac{5\times3}{6\times8}=\frac{15}{48}=\frac{5}{16}$

Exercise 6.5: Multiply fractions with fractions

Use a diagram to determine $\frac{1}{2}\times\frac{2}{5}$ .

Show $\frac{2}{5}$ with a diagram:

Look at $\frac{1}{2}$ : The denominator 2 means each part must be further divided into 2:

The numerator 1 means that we want 1 out of every 2 parts of the shaded area:

The new shading represents $\frac{2}{10}$ .
$\frac{1}{2}\times\frac{2}{5}=\frac{2}{10}=\frac{1}{5}$
Calculate each of the following directly.
1. $\frac{4}{9}\times\frac{3}{5}$
  $\frac{4}{9}\times\frac{3}{5}=\frac{4\times3}{9\times5}=\frac{12}{45}=\frac{4}{15}$
2. $\frac{6}{7}\times\frac{9}{10}$
  $\frac{6}{7}\times\frac{9}{10}=\frac{6\times9}{7\times10}=\frac{54}{70}=\frac{27}{35}$
3. $\frac{11}{12}\times\frac{4}{5}$
  $\frac{11}{12}\times\frac{4}{5}=\frac{11\times4}{12\times5}=\frac{44}{60}=\frac{11}{15}$

Division: whole number ÷ fraction

Suppose there are 4 cakes available for Oluchi's birthday party. The cakes are quite small, so she wants each person to have $\frac{2}{3}$ of a cake. How will Oluchi know how many people will get cake?

Oluchi must calculate $4\div\frac{2}{3}$ . Because she wants each person to get two thirds, $\frac{2}{3}$ , she must start by cutting each cake into 3 pieces.

Now she must work out how many people can each get $\frac{2}{3}$ of a cake.

Worked example 6.10: Dividing using diagrams: whole number ÷ fraction

Calculate:
$4\div\frac{2}{3}$

Step 1: Represent all the parts of the whole number, according to the denominator of the fraction.

The denominator of the fraction is 3. We must divide 4 shapes into 3 parts each.
Step 2: Determine how many times the numerator of the fraction can be counted.

The numerator is 2. This means every 2 parts represents one count.
Step 3: Write down the answer.

There are 6 different colours. We can count every $\frac{2}{3}$ six times. This means at Oluchi's birthday party, 6 people can each get $\frac{2}{3}$ of a cake.
$4\div\frac{2}{3}=6$

Reciprocals of fractions

Division may be seen as another form of multiplication. Dividing by a fraction is the same as multiplying by the "opposite" of the fraction. The "opposite" of a fraction is called its reciprocal. The reciprocal is the fraction we get when we swap the numerator and the denominator. For example, the reciprocal of $\frac{2}{7}$ is $\frac{7}{2}$ and the reciprocal of $\frac{8}{3}$ is $\frac{3}{8}$ .

reciprocal The "opposite" of a fraction, which we get by swapping the numerator and denominator.

Whole numbers also have reciprocals. We may write any whole number as an improper fraction with the denominator 1. For example, $5=\frac{5}{1}$ and $13=\frac{13}{1}$ . Now we get the reciprocal by swapping the numerator and denominator. The reciprocal of 5 is $\frac{1}{5}$ and the reciprocal of 13 is $\frac{1}{13}$ .

The reciprocal of a fraction is also called its multiplicative inverse. When you multiply a fraction and its multiplicative inverse, the answer is 1.

We may use reciprocals in division that involves fractions.

Worked example 6.11: Using a reciprocal to divide: whole number ÷ fraction

Calculate:
$4\div\frac{2}{3}$

Step 1: Regard division as another form of multiplication.

Dividing by a fraction is the same as multiplying by the reciprocal of the fraction.
$4\div\frac{2}{3}=4\times\frac{3}{2}$
Step 2: Follow the short method for multiplying whole numbers and fractions.

Denominator: $\frac{\phantom{00}}{2}$
Numerator: $4\times3=12$
Calculation:
$\begin{array}{l} \phantom{00}4\times\frac{3}{2}\newline =\frac{4\times3}{2} \newline =\frac{12}{2}\newline =\;6 \end{array}$

Exercise 6.6: Divide whole numbers by fractions

Calculate each of the following.

$2\div\frac{1}{6}$

Multiply by the reciprocal of the fraction.
$\begin{array}{l} \phantom{00}2\times\frac{6}{1}\newline =\frac{2\times6}{1} \newline =\frac{12}{1}\newline =\;12 \end{array}$
$7\div\frac{4}{5}$

Multiply by the reciprocal of the fraction.
$\begin{array}{l} \phantom{00}7\times\frac{5}{4}\newline =\frac{7\times5}{4} \newline =\frac{35}{4}\newline =8\frac{3}{4} \end{array}$
$8\div\frac{3}{4}$

Multiply by the reciprocal of the fraction.
$\begin{array}{l} \phantom{00}8\times\frac{4}{3}\newline =\frac{8\times4}{3} \newline =\frac{32}{3}\newline =10\frac{2}{3} \end{array}$

Division: fraction ÷ whole number

At Ifetayo's birthday party, there is only $\frac{3}{4}$ of one cake left. Ifetayo wants to share this equally between her two best friends, so that they can take it home.

The cake that is left may be represented as follows:

Now Ifetayo must figure out how she is going to share this equally between her two friends.

Worked example 6.12: Dividing using a diagram: fraction ÷ whole number

Calculate:
$\frac{3}{4}\div2$

Step 1: Use a diagram to represent the fraction.
Step 2: Divide the shape further, according to the whole number.

The whole number is 2. If we want to share the shaded portion between 2 people, we must divide each shaded part into 2 parts.
Step 3: Share the shaded parts equally, according to the whole number.

The whole number is 2. If we want to share the shaded parts equally between 2 people, we simply allocate them to person 1 and person 2.
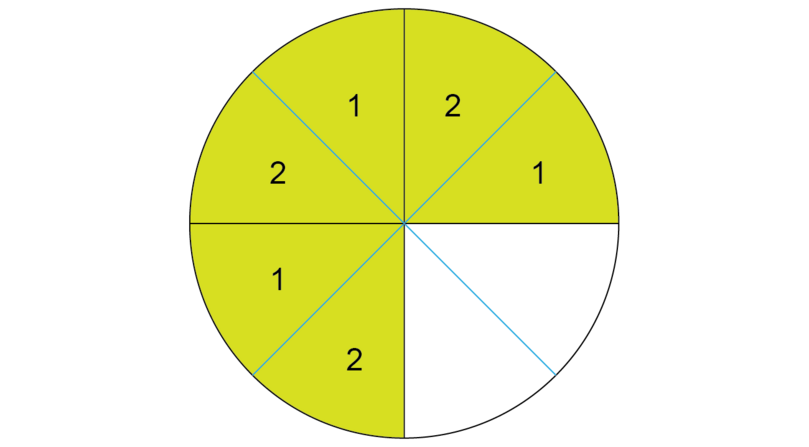
Step 4: Write down the fraction that each person gets.

If we divide $\frac{3}{4}$ between two people, each person gets $\frac{3}{8}$ .
Step 5: Write down the answer.
$\frac{3}{4}\div2=\frac{3}{8}$

Worked example 6.13: Using a reciprocal to divide: fraction ÷ whole number

Calculate:
$\frac{3}{4}\div2$

Step 1: Regard division as another form of multiplication.

Dividing by a whole number is the same as multiplying by the reciprocal of the whole number.
$\frac{3}{4}\times\frac{1}{2}$
Step 2: Follow the short method for multiplying fractions with fractions.
$\frac{3}{4}\times\frac{1}{2}=\frac{3\times1}{4\times2}=\frac{3}{8}$

Exercise 6.7: Divide fractions by whole numbers

Calculate each of the following.

$\frac{4}{5}\div6$

Multiply by the reciprocal of the whole number.
$\frac{4}{5}\times\frac{1}{6}=\frac{4\times1}{5\times6}=\frac{4}{30}=\frac{2}{15}$
$\frac{6}{15}\div4$

Multiply by the reciprocal of the whole number.
$\frac{6}{15}\times\frac{1}{4}=\frac{6\times1}{15\times4}=\frac{6}{60}=\frac{1}{10}$
$\frac{8}{9}\div 10$

Multiply by the reciprocal of the whole number.
$\frac{8}{9}\times\frac{1}{10}=\frac{8\times1}{9\times10}=\frac{8}{90}=\frac{4}{45}$

Division: fraction ÷ fraction

Remember that there was only $\frac{3}{4}$ of one cake left at Ifetayo's birthday party. Suppose, instead of dividing this between her two best friends, she rather decides to give $\frac{1}{8}$ of the cake to as many people as possible.

We already know the cake that is left may be represented as follows:

Now Ifetayo must figure out how many people can get $\frac{1}{8}$ of the cake to take home. She must calculate $\frac{3}{4}\div\frac{1}{8}$ .

Worked example 6.14: Using a diagram to divide: fraction ÷ fraction

Calculate:
$\frac{3}{4}\div\frac{1}{8}$

Step 1: Use a diagram to represent the first fraction.
Step 2: Divide the shape further, until the parts are equal to the denominator of the second fraction.

The denominator of the second fraction is 8.
Step 3: Determine how many times the numerator of the second fraction can be counted from the shaded parts.

The numerator of the second fraction is 1. This means every part represents one count. Remember that we can only count shaded parts.
Step 4: Write down the answer.

There are six different colours. We can count every $\frac{1}{8}$ six times. This means that 6 people can each take home $\frac{1}{8}$ of the cake.
$\frac{3}{4}\div\frac{1}{8}=6$

Worked example 6.15: Using a reciprocal to divide: fraction ÷ fraction

Calculate:
$\frac{3}{4}\div\frac{1}{8}$

Step 1: Regard division as another form of multiplication.

Dividing by a fraction is the same as multiplying by the reciprocal of the fraction.
$\frac{3}{4}\times\frac{8}{1}$
Step 2: Follow the short method for multiplying fractions with fractions.
$\frac{3}{4}\times\frac{8}{1}=\frac{3\times8}{4\times1}=\frac{24}{4}=6$

Exercise 6.8: Divide fractions by fractions

Calculate each of the following.

$\frac{3}{7}\div\frac{1}{2}$

Multiply by the reciprocal of the second fraction.
$\frac{3}{7}\times\frac{2}{1}=\frac{3\times2}{7\times1}=\frac{6}{7}$
$\frac{10}{13}\div\frac{3}{4}$

Multiply by the reciprocal of the second fraction.
$\frac{10}{13}\times\frac{4}{3}=\frac{10\times4}{13\times3}=\frac{40}{39}=1\frac{1}{39}$
$\frac{12}{15}\div\frac{3}{5}$

Multiply by the reciprocal of the second fraction.
$\frac{12}{15}\times\frac{5}{3}=\frac{12\times5}{15\times3}=\frac{60}{45}=\frac{4}{3}=1\frac{1}{3}$

Multiplying and dividing mixed numbers

There are various methods that may be used to multiply and divide mixed numbers. It is recommended that you first convert all mixed numbers to improper fractions before you multiply or divide.

If necessary, go back to Chapter 4 and revise how to convert mixed numbers to improper fractions.

Simplifying before multiplying

Improper fractions sometimes involve large numbers that are not so easy to multiply. To make things easier, you should try to simplify the numerators and denominators before you multiply them.

Note that the order in which we multiply numbers do not affect the answer. For example:

$3\times5=15$ and $5\times3=15$
$\frac{4}{5}\times\frac{1}{3}=\frac{4}{15}$ and $\frac{1}{3}\times\frac{4}{5}=\frac{4}{15}$

In Chapter 4 you learnt that equivalent factors have the same value. We find equivalent factors by multiplying or dividing the numerator and denominator by the same number. For example:

$\frac{12\div2}{16\div 2}=\frac{6}{8}$

$\frac{6\div2}{8\div2}=\frac{3}{4}$

Worked example 6.16: Dividing mixed numbers

Calculate:
$2\frac{5}{8}\div3\frac{3}{4}$

Step 1: Convert the mixed numbers to improper fractions.
$2\frac{5}{8}=\frac{(8\times2)+5}{8}=\frac{21}{8}$ $3\frac{3}{4}=\frac{(4\times3)+3}{4}=\frac{15}{4}$
Step 2: Regard division as another form of multiplication.

Dividing by a fraction is the same as multiplying by the reciprocal of the fraction.
$\frac{21}{8}\times\frac{4}{15}$
Step 3: Write down the first step for multiplying fractions by fractions. Then see whether there are numerator and denominator pairs that have common factors.

The first step is:
$\frac{21\times4}{8\times15}$
The HCF of 4 and 8 is 4.
The HCF of 21 and 15 is 3.

If necessary, go back to Chapter 2 to revise how to find the highest common factor (HCF) of two or more numbers.

Write the pairs underneath each other. Remember, we may multiply numbers in any order.
$\frac{\color{red}{4}\; \color{black}{\times}\; \color{green}{21}}{\color{red}{8}\; \color{black}{\times}\;\color{green}{15}}$
Step 4: Divide by the common factors you identified in Step 3.

We may find equivalent fractions by dividing a numerator and denominator by the same number.
$\frac{\color{red}{4\div4}\; \color{black}{\times}\; \color{green}{21\div3}}{\color{red}{8\div4}\; \color{black}{\times}\;\color{green}{15\div3}}$
Step 5: Write down the simplified expression and calculate the answer.
$\frac{1\times7}{2\times5}=\frac{7}{10}$
Step 6: Check that the answer is in its simplest form. Write improper fractions as mixed numbers.

In this case, the answer is in its simplest from.

If necessary, go back to Chapter 4 and revise how to convert improper fractions to mixed numbers.

Exercise 6.9: Multiply and divide mixed numbers

Calculate the following.

$5\frac{1}{3}\times2\frac{3}{4}$
$5\frac{1}{3}=\frac{(3\times5)+1}{3}=\frac{16}{3}$ $2\frac{3}{4}=\frac{(4\times2)+3}{4}=\frac{11}{4}$ $\frac{16}{3} \times \frac{11}{4}= \frac{16\times11}{3\times4}$
The HCF of 16 and 4 is 4.
$\frac{(16\div4)\times11}{(4\div4)\times3}=\frac{4\times11}{1\times3}=\frac{44}{3}=14\frac{2}{3}$
$3\frac{3}{5}\times1\frac{6}{9}$
$3\frac{3}{5}=\frac{(5\times3)+3}{5}=\frac{18}{5}$ $1\frac{6}{9}=\frac{(9\times1)+6}{9}=\frac{15}{9}$ $\frac{18}{5} \times \frac{15}{9}= \frac{18\times15}{5\times9}$
The HCF of 18 and 9 is 9.
The HCF of 15 and 5 is 5.
$\frac{(18\div9)\times(15\div5)}{(9\div9)\times(5\div5)}=\frac{2\times3}{1\times1}=\frac{6}{1}=6$
$7\frac{1}{8}\div4\frac{3}{4}$
$7\frac{1}{8}=\frac{(8\times7)+1}{8}=\frac{57}{8}$ $4\frac{3}{4}=\frac{(4\times4)+3}{4}=\frac{19}{4}$ $\frac{57}{8}\div\frac{19}{4}=\frac{57}{8} \times \frac{4}{19}= \frac{57\times4}{8\times19}$
The HCF of 4 and 8 is 4.
The HCF of 57 and 19 is 19.
$\frac{(57\div19)\times(4\div4)}{(19\div19)\times(8\div4)}=\frac{3\times1}{1\times2}=\frac{3}{2}=1\frac{1}{2}$
$4\frac{1}{6}\div3\frac{8}{9}$
$4\frac{1}{6}=\frac{(6\times4)+1}{6}=\frac{25}{6}$ $3\frac{8}{9}=\frac{(9\times3)+8}{9}=\frac{35}{9}$ $\frac{25}{6}\div\frac{35}{9}=\frac{25}{6} \times \frac{9}{35}= \frac{25\times9}{6\times35}$
The HCF of 6 and 9 is 3.
The HCF of 35 and 25 is 5.
$\frac{(25\div5)\times(9\div3)}{(35\div5)\times(6\div3)}=\frac{5\times3}{7\times2}=\frac{15}{14}=1\frac{1}{14}$
$6\frac{3}{10}\div1\frac{4}{5}$
$6\frac{3}{10}=\frac{(10\times6)+3}{10}=\frac{63}{10}$ $1\frac{4}{5}=\frac{(5\times1)+4}{5}=\frac{9}{5}$ $\frac{63}{10}\div\frac{9}{5}=\frac{63}{10} \times \frac{5}{9}= \frac{63\times5}{10\times9}$
The HCF of 5 and 10 is 5.
The HCF of 63 and 9 is 9.
$\frac{(63\div9)\times(5\div5)}{(9\div9)\times(10\div5)}=\frac{7\times1}{1\times2}=\frac{7}{2}=3\frac{1}{2}$

6.3 Practical applications

You can use your knowledge of fractions to solve problems. Here are some hints:

Remember that the denominator of a fraction tells us how many parts a whole is divided into. The numerator tells us how many of those parts we are dealing with.
Read the problem carefully. If at all possible, draw a diagram to represent the situation.
Percentages are fractions. For example, 70% of 25 may be written as $\frac{70}{100}\times25$ .
A whole, for example all the sweets or the full length of time or all the money, is represented by the number 1.
Decide whether you must add, subtract, multiply or divide:
- "find the sum" means you must add
- "find the difference" means you must subtract
- "of" means you must multiply
- "share between" means you must divide

Exercise 6.10: Use operations with fractions to solve problems

Chijindum spends $\frac{1}{4}$ of his pocket money on clothes and $\frac{3}{10}$ on sweets. What fraction of his pocket money did he spend altogether?

$\begin{array}{l} \phantom{00}\frac{1}{4}+\frac{3}{10} \newline =\frac{5}{20}+\frac{6}{20} \newline =\frac{5+6}{20} \newline =\frac{11}{20} \end{array}$
Chijindum spends $\frac{11}{20}$ of his pocket money altogether.
It takes Adanna $\frac{5}{8}$ Â of an hour to walk to school. How long will it take her to walk to school, back home and back to school again?

$\begin{array}{l} \phantom{00}\frac{5}{8}\times3 \newline =\frac{5\times3}{8} \newline =\frac{15}{8} \newline =1\frac{7}{8}\space\text{hours} \newline \end{array}$
It will take Adanna $1\frac{7}{8}$ Â hours.
In a certain class, $\frac{5}{8}$ of the class are girls and $\frac{9}{10}$ of the girls take Mathematics. Calculate the fraction of the class that are girls and take Mathematics.

$\frac{9}{10}\times\frac{5}{8}=\frac{9\times5}{10\times8}=\frac{45}{80}=\frac{9}{16}$
$\frac{9}{16}$ of the class are girls and take Mathematics.
Only $\frac{9}{10}$ of the Mathematics class came to school on Friday. At the start of the lesson, the principal called $\frac{1}{6}$ of the class to his office. What fraction of the class had Mathematics on Friday?

$\begin{array}{l} \phantom{00}\frac{9}{10}-\frac{1}{6} \newline =\frac{27}{30}-\frac{5}{30} \newline =\frac{27-5}{30} \newline =\frac{22}{30} \newline =\frac{11}{15} \end{array}$
$\frac{11}{15}$ of the class had Mathematics on Friday.
Talatu decides to share a packet of sweets with her siblings. She gives $\frac{1}{4}$ of the packet to her sister and $\frac{3}{8}$ to her brother. What fraction of the sweets does she keep for herself?

$\begin{array}{l} \phantom{00}1-\frac{1}{4}-\frac{3}{8} \newline =\frac{8}{8}-\frac{2}{8}-\frac{3}{8} \newline =\frac{8-2-3}{8} \newline =\frac{3}{8} \newline \end{array}$
Talatu kept $\frac{3}{8}$ of the sweets for herself.
A local store owner buys rice in bags of 50Â kg. He then makes up smaller bags to sell. If a small bag is $\frac{6}{15}$ Â kg, how many small bags can he make up from one large bag?

$\begin{array}{l} \phantom{00}50\div\frac{6}{15} \newline =50\times\frac{15}{6} \newline =\frac{50\times15}{6} \newline =\frac{750}{6} \newline =\;125\ \end{array}$
The store owner can make up 125 small bags from one large bag.
There is $\frac{14}{16}$ Â litre of vegetable oil left in a bottle. A baker must measure this out in cups of $\frac{1}{4}$ Â litre each. How many cups will she measure out?

$\frac{14}{16}\div\frac{1}{4}=\frac{14}{16}\times\frac{4}{1}=\frac{14\times4}{16\times1}=\frac{56}{16}=\frac{7}{2} =3\frac{1}{2}$
The baker can measure out $3\frac{1}{2}$ cups.
Habib goes home after school. He spends a $\frac{1}{5}$ Â hour having lunch, then watches television for $1\frac{2}{3}$ Â hours, and then does his homework for $2\frac{1}{6}$ Â hours. How long did all these activities take?

$\begin{array}{l} \phantom{00}\frac{1}{5}+1\frac{2}{3}+2\frac{1}{6} \newline =\frac{1}{5}+\frac{5}{3}+\frac{13}{6} \newline =\frac{6}{30}+\frac{50}{30}+\frac{65}{30} \newline =\frac{6+50+65}{30} \newline =\frac{121}{30} \newline =4\frac{1}{30}\space\text{hours} \end{array}$
These activities take $4\frac{1}{30}$ hours.
A clothing store offers a discount of 15% on a pair of shoes that originally cost ₦1,500. Calculate the new, discount price.

$\begin{array}{l} \phantom{000}15\%\times1,500 \newline =\frac{15}{100}\times1,500 \newline =\frac{15\times1,500}{100} \newline =\frac{15\times15}{1} \newline =\frac{225}{1} \end{array}$
The new, discount price is $₦1,500-₦225=₦1,275$ .
A bag of garri has a mass of $10\frac{5}{6}$ Â kg. How many small packets, each with a mass of $2\frac{1}{2}$ Â kg, can be made up from the bag?

$10\frac{5}{6}=\frac{65}{6}$ $2\frac{1}{2}=\frac{5}{2}$ $\frac{65}{6}\div\frac{5}{2}=\frac{65}{6} \times \frac{2}{5}= \frac{65\times2}{6\times5}$ $\frac{(65\div5)\times(2\div2)}{(5\div5)\times(6\div2)}=\frac{13\times1}{1\times3}=\frac{13}{3}=4\frac{1}{3}$
$4\frac{1}{3}$ small packets can be made up.

6.6 Summary

To add or subtract fractions with the same denominator:
- Write down the denominator.
- Then add or subtract the numerators.
To add or subtract fractions with different denominators:
- Find the LCD.
- Find equivalent fractions with the LCD as denominator.
- Then add or subtract the numerators.
To multiply fractions and whole numbers:
- Write down the denominator of the fraction.
- Multiply the numerator of the fraction by the whole number.
To multiply fractions with fractions:
- Multiply the numerators.
- Multiply the denominators.
The reciprocal of a fraction is the "opposite" of the fraction, which we get by swapping the numerator and denominator. Whole numbers also have reciprocals. For example:
- The reciprocal of $\frac{4}{9}$ is $\frac{9}{4}$ .
- The reciprocal of 8 is $\frac{1}{8}$ .
Dividing by a fraction or whole number is the same as multiplying by its reciprocal. For example:
- $\frac{4}{9}\div 8=\frac{4}{9}\times\frac{1}{8}$
- $\frac{4}{9}\div \frac{3}{5}=\frac{4}{9}\times\frac{5}{3}$
Before you add, subtract, multiply or divide mixed numbers, first convert them to improper fractions.
When you have to multiply fractions with large numerators or denominators, simplify first.

Chapter 5: Addition and subtraction of integers

Table of Contents

Chapter 7: Estimation and approximation

Test yourself now

Chapter 6: Operations with fractions

6.1 Addition and subtraction of fractions

Adding fractions with the same denominator

Subtracting fractions with the same denominator

Worked example 6.1: Adding fractions with the same denominator

Worked example 6.2: Subtracting fractions with the same denominator

Exercise 6.1: Add and subtract fractions that have the same denominators

Adding and subtracting fractions with different denominators

Worked example 6.3: Adding fractions with different denominators

Worked example 6.4: Subtracting fractions with different denominators

Exercise 6.2: Add and subtract fractions that have different denominators

Adding and subtracting mixed numbers

Worked example 6.5: Adding mixed numbers

Exercise 6.3: Add and subtract mixed numbers

6.2 Multiplication and division of fractions

Multiplication: whole number x fraction

Worked example 6.6: Multiplying: whole number x fraction

Multiplication: fraction x whole number

Worked example 6.7: Multiplying: fraction x whole number

Exercise 6.4: Multiply fractions and whole numbers

Multiplication: fraction x fraction

Worked example 6.8: Multiplying using a diagram: fraction x fraction

Worked example 6.9: Calculating fraction x fraction directly

Exercise 6.5: Multiply fractions with fractions

Division: whole number ÷ fraction

Worked example 6.10: Dividing using diagrams: whole number ÷ fraction

Reciprocals of fractions

Worked example 6.11: Using a reciprocal to divide: whole number ÷ fraction

Exercise 6.6: Divide whole numbers by fractions

Division: fraction ÷ whole number

Worked example 6.12: Dividing using a diagram: fraction ÷ whole number

Worked example 6.13: Using a reciprocal to divide: fraction ÷ whole number

Exercise 6.7: Divide fractions by whole numbers

Division: fraction ÷ fraction

Worked example 6.14: Using a diagram to divide: fraction ÷ fraction

Worked example 6.15: Using a reciprocal to divide: fraction ÷ fraction

Exercise 6.8: Divide fractions by fractions

Multiplying and dividing mixed numbers

Simplifying before multiplying

Worked example 6.16: Dividing mixed numbers

Exercise 6.9: Multiply and divide mixed numbers

6.3 Practical applications

Exercise 6.10: Use operations with fractions to solve problems

6.6 Summary